理论物理：拓扑场论和二维量子引力【转载】

本文目录

1. 引言

过去几年见证了量子场论技术在研究各种数学问题上丰硕的应用。这个主要归功于Edward Witten的项目，已经找到了量子场论和拓扑与几何量间意想不到的关联。这点的精彩范例是，三维规范理论和二维共形场论中出现了像Jones多项式这样的纽结不变量^[1]。直到最近，这些发展也主要是带给我们，要么是新的数学上的不变量，要么是对从量子场论的直觉得到的结果的更好理解。用在这些构造中的量子场论，虽然是更物理的场论的近亲，但没有直接的物理应用。

随着对矩阵模型和一般的二维量子引力的研究，意想不到的转机出现了。一个称为拓扑引力^[2]的特殊场论，最初被构造来处理Riemann面模空间的问题，被证明与二维量子引力有密不可分的关联。可将它看成引力的另一个更简单的相，其中关联函数更容易计算。借助矩阵模型在二维引力中取得重大突破^[3]后不久，Witten指出量子引力可能不过是拓扑引力的简单微扰^[4]。这点现在已经有了坚实的证据，提供了从拓扑引力开始得到所有矩阵模型结果的相当直接的方法^[4]^[5]^[6]^[7]^[8]^[9]。拓扑引力有个推广，称为拓扑弦论，其中引力与各种物质系统耦合^[4]。拓扑弦论可用于描述和解与引力耦合的所有 $c<1$ 极小模型，以及很多其它理论^[10]^[11]^[12]^[13]。

这份讲义旨在对一般的拓扑场论，特别是拓扑引力进行初步介绍。我们的最终目标，是建立起与矩阵模型结果的关联，特别是可积的KdV型层次结构^[14]^[15]的出现。不过，最后一节才会涉及这点。沿途我们将讨论几何，代数和量子场论间诸多优美的关联。

这份讲义中，描述与E. 和H. Verlinde，以及与E. Witten合作的工作的部分，将基本照着同一主题其它已出版的讲义^[16]，但有些地方可能更加友好。这份讲义会和在冬季学校讲的四节课高度一致，也是依此来组织的。在第2节，我们讨论拓扑场论的一些一般性质。我们强调因子化的概念，并应用于二维情形。在第3节，我们考虑拓扑共形场论，它们与 $\mathcal{N}=2$ 超对称模型密切相关，并为上节的抽象讨论提供一些例子。拓扑引力放在第4节，那里我们还将用递归关系讨论它的解。最后，在第5节，我们讨论与矩阵模型和可积KdV层次结构的关联。

2. 拓扑场论

拓扑场论由Witten^[17]^[18]引入。（综述可见^[19]^[20]。）本节选取的拓扑场论方法中，我们将直接关注量子场论中有趣的可测量：物理算符的关联函数。这种方法不是从作用量开始，根据路径积分来确定计算关联函数的规则，而是利用理论中巨量的对称性直接计算关联函数。这样就不必处理作用量形式中出现的冗余信息：众所周知，对同一个物理模型，作用量可能不止一个。因此我们的方法有些“自举”的味道，像是D. Gross最喜欢说的“无中生有”，可能会让一些读者不适。按这种精神，我们以一些相当一般的评论开启讨论。

2.1 拓扑不变性

量子场论与几何间的关联，可表述成相当一般的形式。局域量子场论的性质之一，就是可表述在任意形状的时空中。（即使号差是Euclid型或根本未定义时，我们也经常会用“时空”这个词，以提醒读者有可能在局域引入时间流，对时空切片，引入量子态的Hilbert空间和作用在这些态上的Hamiltonian。）研究唯象上有趣的量子场论时，我们不会首先考虑拓扑复杂的时空，因为我们主要关心局域性质，例如不同量子场间的相互作用。然而，在拓扑场论中，重要的只有全局性质，没有模式在传播，考虑任意拓扑的时空至关重要。事实上，时空的拓扑是拓扑场论中少数几个可测量之一。

给定紧 $D$ 维时空流形 $M$ ，以及带一组基本场 $\phi(x)$ 的量子场论，我们可以考虑真空振幅

$Z(M)=\int[d \phi] e^{-S[\phi]}\quad \quad (2.1)$

这里将 $Z(M)$ 形式上定义成，作用量 $S$ 加权的，对定义在 $M$ 上所有场构型的路径积分。然而，很多时候 $S$ 不是具体的，我们只是将 $Z(M)$ 看成某个给定的量，最终将用不同方法来计算。一般来说，配分函数 $Z(M)$ 依赖于流形上的额外结构。例如，在几乎所有已知的量子场论中，我们需要Riemann结构，也就是度规 $g_{\mu\nu}$ ，有时还需要 $M$ 的定向。其它的可能包括：有费米子时需要自旋结构，有规范场时需要纤维丛……尽管在表述时，量子场论可能看上去依赖于编码在度规 $g_{\mu\nu}(x)$ 中的所有信息，但实际上振幅还是可能在度规的某些变换下不变。一个例子当然是重参数化

$\delta g_{\mu \nu}(x)=\nabla_{\mu} \epsilon_{\nu}(x)+\nabla_{\nu} \epsilon_{\mu}(x)\quad \quad (2.2)$

下的不变性。大家都知道，这给出守恒律

$\nabla^{\mu} T_{\mu \nu}=0\quad \quad (2.3)$

其中能动张量

$T_{\mu \nu}=\frac{1}{\sqrt{g}} \frac{\delta S}{\delta g^{\mu \nu}}\quad \quad (2.4)$

编码了量子场论在度规形变下的变化。

读者会熟悉的另一个例子是共形不变性：在度规局域重标度

$\delta g_{\mu \nu}(x)=\epsilon(x) g_{\mu \nu}(x)\quad \quad (2.5)$

下的不变性。这给出 $T_{\mu\nu}$ 无迹：

$T^{\mu}{}_{\mu}=0\quad \quad (2.6)$

如果一个量子场论在度规的任意光滑形变

$\delta g_{\mu \nu}(x)=\epsilon_{\mu \nu}(x)\quad \quad (2.7)$

下不变，就称为拓扑的。这时重要的只有流形 $M$ 的拓扑，配分函数 $Z(M)$ 是拓扑不变量。能动张量必须完全为零：

$T_{\mu \nu}=0 \quad \quad (2.8)$

这里的讨论可从真空振幅推广到物理的关联函数。在一般的量子场论中，关联函数依赖于算符的位置，时空的度规，定向和拓扑，还可能有许多其它的。但在拓扑场论中，局域算符的物理关联函数只是些数字：

$\left\langle\phi_{i_{1}}\left(x_{1}\right) \phi_{i_{2}}\left(x_{2}\right) \ldots \phi_{i_{s}}\left(x_{s}\right)\right\rangle_{M}=常数\quad \quad(2.9)$

它们不依赖于时空 $M$ 中的度规 $g_{\mu\nu}$ 和算符的位置 $x_i$ ，只依赖于算符的数目和类型，以及 $M$ 的拓扑。我们已经看到，由于不依赖于度规，能动张量在物理的关联函数中应当为零：

$\left\langle T_{\mu \nu}(x) \phi_{i_{1}}\left(x_{1}\right) \cdots \phi_{i_{s}}\left(x_{s}\right)\right\rangle=0\quad \quad (2.10)$

有多种方式来实现这条件。在常规的量子引力中，令度规成为动力学的，然后对所有度规作路径积分，以实现广义协变性：

$T_{\mu \nu}=T_{\mu \nu}^{物质}+T_{\mu \nu}^{引力}=0\quad \quad (2.11)$

物质的能动张量被引力的抵消了。

我们将用另一种方式实现广义协变性，不引入动力学度规。它将是一个费米对称性的结果，这由荷 $Q$ 生成。像BRST荷一样， $Q$ 是幂零的：

$Q^2=0\quad \quad (2.12)$

但我们将在很多例子中看到， $Q$ 不必对应BRST对称性。我们假定模型具有 $Q$ 生成的对称性，这就要求真空被 $Q$ 湮灭。现在可在整个态的Hilbert空间 $\mathcal{H}$ 中定义物理的子空间 $\mathcal{H}_{物理}$ ：

$\mathcal{H}_{物理}=\frac{\operatorname{ker} Q}{\operatorname{im} Q}=\left\{\phi_{i} \in \mathcal{H} \mid\left\{Q, \phi_{i}\right\}=0, \quad \phi_{i} \equiv \phi_{i}+\{Q, \lambda\}\right\} \quad \quad (2.13)$

（这里不区分态和局域算符。）因此，物理态对应 $Q$ 的上同调类： $Q$ -闭的态模去 $Q$ -恰当的态。具体将哪个算符取成代表元无关紧要，因为一个众所周知的论证表明，非物理的态（形如 $\{Q,\lambda\}$ 的态）在物理的关联函数中解耦。

存在算符 $Q$ 当然不足以保证广义协变性，我们还需要另一个重要条件，也就是能动张量 $T_{\mu\nu}$ 非物理：

$T_{\mu \nu}=\left\{Q, G_{\mu \nu}\right\} \quad \quad (2.14)$

要求 $T_{\mu\nu}$ 是 $Q$ -恰当的，就保证了 $(2.10)$ ，我们将会频繁借助这关系。算符 $G_{\mu\nu}$ 也是二阶张量，但反对易。 $T_{\mu\nu}$ 和 $G_{\mu\nu}$ 对应的守恒荷是

$P_{\mu}=\int d^{D-1} x T_{\mu 0}(x), \quad G_{\mu}=\int d^{D-1} x G_{\mu 0}(x)\quad \quad (2.15)$

积分是在 $D$ 维时空 $M$ 的一个类空曲面上作的。这些荷给出平移群的反对易扩张：

$P_{\mu}=\left\{Q, G_{\mu}\right\}, \quad\left\{G_{\mu}, G_{\nu}\right\}=0\quad \quad (2.16)$

也可进一步构造整个Poincaré代数的扩张。这会类似于超Poincaré代数，但 $Q$ 的自旋是0而不是1/2。

2.2 下降方程

将 $Q$ 对称性看成自旋0超对称，会给出丰硕的结果。事实上，理论用“超空间”表述会很方便，这将在模型中自然地给出非局域的可测量。除了时空坐标 $x^\mu$ ，我们现在还有 $D$ 个Grassmann坐标 $\theta^\mu$ 。从物理场 $\phi(x)$ （有时记作 $\phi^{(0)}(x)$ ，以表示它是局域算符）开始，得到超场

$\Phi(x, \theta)=e^{\theta^{\mu} G_{\mu}} \phi(x)=\phi^{(0)}(x)+\phi_{\mu}^{(1)}(x) \theta^{\mu}+\ldots+\phi_{\mu_{1} \ldots \mu_{D}}^{(D)}(x) \theta^{\mu_{1}} \cdots \theta^{\mu_{D}}\quad \quad (2.17)$

场 $\phi^{(n)}$ 由 $\phi^{(0)}$ 多次作用上 $G_\mu$ 生成：

$\phi_{\mu_{1} \ldots \mu_{n}}^{(n)}(x)=\left\{G_{\mu_{1}},\left\{G_{\mu_{2}}, \ldots,\left\{G_{\mu_{n}}, \phi^{(0)}(x)\right\} \ldots\right\}\right\}\quad \quad (2.18)$

括号 $\{\cdot \}$ 视情况代表对易子或反对易子。因为 $\phi_{\mu_{1} \ldots \mu_{n}}^{(n)}(x)$ 关于指标反对称，它代表一个时空 $n$ -形式。这些微分形式满足重要的下降方程

$d \phi^{(n)}=\left\{Q, \phi^{(n+1)}\right\}\quad \quad (2.19)$

这是从 $Q$ 湮灭 $\phi^{(0)}$ 且作用在 $G_\mu$ 上给出 $P_\mu$ 推出的，例如

$\left\{Q, \phi_{\mu}^{(1)}\right\}=\left\{Q,\left\{G_{\mu}, \phi^{(0)}\right\}\right\}=\left\{P_{\mu}, \phi^{(0)}\right\}=\partial_{\mu} \phi^{(0)}\quad \quad (2.20)$

用超场写，下降方程的形式更简单：

$D \Phi=0, \quad\quad D=Q-\theta^{\mu} \frac{\partial}{\partial x^{\mu}}\quad \quad (2.21)$

因此 $Q$ 像是作用在物理场上的外导数 $d$ ，这点很有用。

从下降方程可以看出两件事。第一，它暗示存在一类新的物理算符。下降方程 $(2.19)$ 表明， $Q$ 作用在 $\phi^{(n)}$ 上给出恰当形式。这在闭链上积分为零，因此如果 $C$ 是 $n$ 维无边（ $\partial C=0$ ）子流形，那么

$\int_{C} \phi^{(n)}$

是物理算符：

$\left\{Q, \int_{C} \phi^{(n)}\right\}=\int_{C} d \phi^{(n-1)}=\int_{\partial C} \phi^{(n-1)}=0\quad \quad (2.22)$

虽然这些 $n$ -形式的积分是物理算符，但它们是非局域的，应当看成Wilson圈算符的高维推广。只有 $\phi^{(0)}$ 是局域算符，可以插在一点上而不破坏广义协变性。

图1：如果在时空$M$中，两$n$维子流形$C,C^\prime$是$n+1$维流形$S$的边界，那么非局域算符$\int_C \phi^{(n)}$和$\int_{C^\prime} \phi^{(n)}$作为物理可测量是等价的。

第二是可以看出，这些积分算符在多大程度上依赖于在其上积分的子流形。考虑两个子流形 $C$ 和 $C'$ 的情形。令它们作为另一个 $n+1$ 维子流形 $S$ 的边界，如图1。由Stokes定理和下降方程，我们有

$\int_{C} \phi^{(n)}-\int_{C^{\prime}} \phi^{(n)}=\int_{S} d \phi^{(n)}=\left\{Q, \int_{S} \phi^{(n+1)}\right\}\quad \quad (2.23)$

因此这物理可测量只依赖于 $C$ 的上同调类。也就是说，对 $H_n(M)$ 中每类，都能构造一个非局域算符。在0-形式场的情形，我们有

$\phi^{(0)}(x)-\phi^{(0)}(y)=\int_{x}^{y} d x^{\mu}\left\{Q, \phi_{\mu}^{(1)}\right\}\quad \quad (2.24)$

这明确地表明了我们说的，局域物理算符的关联函数不依赖于位置。一个总存在的非常重要的非局域算符，是最高次形式

$\int_{M} \phi^{(D)}\quad \quad (2.25)$

因为 $\phi^{(D)}$ 是体积形式，可在时空本身中积分。这样就可调整作用量，在作用量 $S$ 中加上带些耦合常数 $t$ 的 $(2.25)$ ：

$S \rightarrow S-t \int_{M} \phi^{(D)}\quad \quad (2.26)$

而不破坏广义协变性。之后将看到，这点非常重要。

2.3 超对称，扭和Donaldson理论

我们已经看到，拓扑场论中可以有满足如下关系的守恒荷：

$P_{\mu}=\left\{Q, G_{\mu}\right\}\quad \quad (2.27)$

这让我们想起标准的超对称代数

$P_{\mu} \sigma_{\alpha \beta}^{\mu}=\left\{Q_{\alpha}, \bar{Q}_{\beta}\right\}\quad \quad (2.28)$

唯一的不同在于超对称荷的Lorentz结构： $(2.28)$ 中是自旋1/2， $(2.27)$ 中则是自旋0和1。如果可以改变荷的自旋，就能从超对称理论中得到拓扑理论。一种调整Lorentz指标的方式是，将Lorentz群同一个内部对称群混合起来，在这个群的作用下，超对称荷以非平凡的方式变换。这样的操作称为“扭”，在Donaldson理论^[17]的情形首次观察到。

Donaldson理论与扭 $D=4,\mathcal{N}=2$ 超Yang-Mills理论有关。Witten引入它作为拓扑场论的第一个例子。四维Euclid时空中的Lorentz群是 $S O(4)=S U(2)_{L} \times S U(2)_{R}$ ，由流 $J^L,J^R$ 生成，超荷按内部对称群 $SU(2)_I$ 的某个表示变换，对应流 $J^I$ 。用分量写是 $Q_{\alpha}^{a}$ 和 $\bar{Q}_{\dot{\alpha}}^{a}$ ，这里的指标表明荷是 $SU(2)_I$ 旋量，同时也分别是 $SU(2)_L$ 和 $SU(2)_R$ 旋量。用流写，如果将Lorentz群的作用调成

$J^{R} \rightarrow J^{R}+J^{I}\quad \quad (2.29)$

也就是将 $SU(2)_R$ 换成 $SU(2)_R\times SU(2)_I$ 的对角子群，超荷 $\bar{Q}_{\dot{\alpha}}^{a}$ 就按 $\mathbf{2}\times \mathbf{2}=\mathbf{1}+\mathbf{3}$ 分解：

$\bar{Q}_{\dot{\alpha}}^{a} \rightarrow Q+Q_{i}\quad \quad (2.30)$

标量 $Q$ 是幂零的，因此这种荷就是构造拓扑场论需要的。这样就可从 $\mathcal{N}=2$ 理论得到自旋0超对称。这样的扭操作非常有力，虽然我们的例子是四维，但在第3节更深入地考察二维拓扑场论时还将遇到它。

2.4 基态和物理态

回到一般的拓扑场论，我们想展示，物理态对应理论的基态，也就是能量 $\epsilon=0$ 的。（当然，从理论不依赖于度规，这就已经显然了。因为没法定义长度，就没有时间，也就没有能量。）首先注意到， $G_0$ 是Hamiltonian $H=P_0$ 的 $Q$ 伙伴：

$H=\left\{Q, G_{0}\right\}, \quad[H, Q]=0\quad \quad (2.31)$

现在可以立刻看到物理态是基态。假定某个态 $|\phi \rangle$ 的能量 $\epsilon \neq 0$ ，那么

$|\phi\rangle=\frac{1}{\epsilon} H|\phi\rangle=\frac{1}{\epsilon} Q G_{0}|\phi\rangle=Q|\lambda\rangle\quad \quad (2.32)$

其中 $|\lambda\rangle=G_0|\phi\rangle/\epsilon$ 。因此 $|\phi\rangle$ 是 $Q$ -恰当的，不可能是物理态，除非对应真空， $\epsilon =0$ ，但这与我们的假定矛盾。反过来，我们想展示所有基态都是物理的。这需要一个正定的内积，使得 $Q^\dagger=G_0$ 。这当然不是Lorentz不变的，因为 $G_0$ 是一个向量的分量，并非标量。存在这样奇怪的内积的话，论证是直接的。如果 $|\phi\rangle$ 是基态，那么

$0=\langle\phi|H| \phi\rangle=\| Q|\phi\rangle \|^{2}+ \| G_{0}|\phi\rangle \|^{2}\quad \quad (2.33)$

于是 $Q|\phi\rangle=0=G_{0}|\phi\rangle$ ， $|\phi\rangle$ 是物理态。之后将看到，这个神秘的内积其实和刚刚讨论的扭有关，并且在我们感兴趣的例子中自然地出现。因此在那些情形，基态和物理态一一对应。

2.5 算符代数和因子化

我们已经强调过，拓扑场论可在一般的代数框架下研究，不需要具体的作用量。关联函数和配分函数被看成给定的量，量子场论提供它们间的关系。理论最重要的代数性质是因子化。这个想法大致是说，我们可将时空 $M$ 沿一个类空 $D-1$ 维曲面 $\Sigma$ 切成 $M_1,M_2$ 两份，原来时空上的关联函数应当是这两份上的乘起来，并对流过边界的态求和。

要更具体地说，我们必须考虑带边的时空 $M$ 。对 $M$ 的边界 $\partial M$ 的每个连通部分 $\Sigma$ ，量子场论为它赋上态的Hilbert空间 $\mathcal{H}_\Sigma$ 。这个Hilbert空间可通过考虑柱 $\Sigma \times \mathbb{R}$ 上的正则量子化来构造， $\Sigma$ 是类空的， $\mathbb{R}$ 是时间方向。态 $|\Psi\rangle \in \mathcal{H}_{\Sigma}$ 是限制在 $\Sigma$ 上的场变量 $\phi(x)$ 的特定波函数 $\Psi(\phi)$ 。一般来说， $\mathcal{H}_\Sigma$ 的定义取决于 $\Sigma$ 的定向。定向相反的流形记作 $-\Sigma$ ，我们有 $\mathcal{H}_{-\Sigma}=\mathcal{H}_{\Sigma}^{*}$ 。如果边界 $\partial M$ 有好几个部分 $\Sigma_{1}, \ldots, \Sigma_{n}$ ，我们定义

$\mathcal{H}_{\partial M}=\mathcal{H}_{\Sigma_{1}} \otimes \cdots \otimes \mathcal{H}_{\Sigma_{n}}\quad \quad (2.34)$

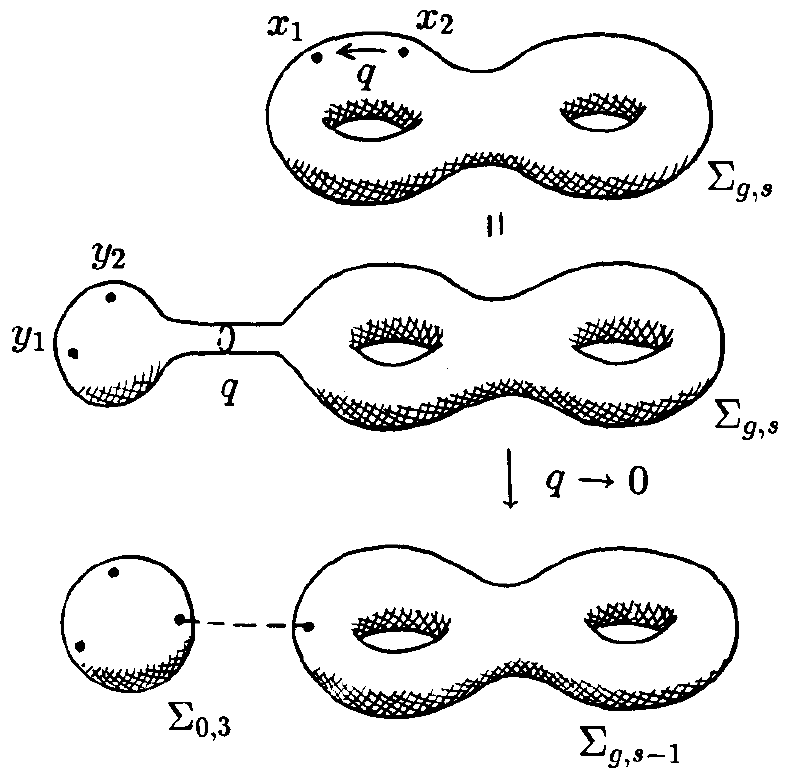
如果所有定向与 $M$ 一致，那么时空 $M$ 会在它的边界对应的Hilbert空间中定义一个特定的态 $|M\rangle \in \mathcal{H}_{\partial M}$ 。直觉上，这个波函数 $\Psi_{M}\left(\phi^{\prime}\right)$ 应定义成对在边界上等于 $\phi'$ 的， $M$ 上所有场构型 $\phi$ 的路径积分，如图2：

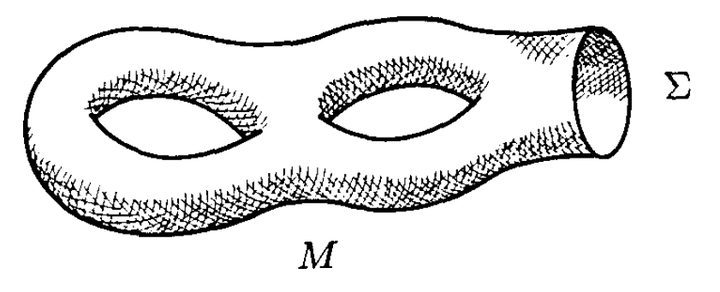
$\Psi_{M}\left(\phi^{\prime}\right)=\int_{\left.\phi\right|_{\partial M}=\phi^{\prime}}[d \phi] e^{-S[\phi]}\quad \quad (2.35)$

图2：如果时空$M$只有一个边界$\Sigma$，量子场论会为$M$赋上Hilbert空间$\mathcal{H}_\Sigma$中的一个态$|M\rangle$。

一般地，我们可以考虑这样的情形： $\partial M$ 的一部分（记作 $\Sigma'$ ），定向与 $M$ 一致，另一部分（ $\Sigma$ ）则相反，如图3。这时， $M$ 上的路径积分会定义一个跃迁振幅

$\Phi_{M}: \mathcal{H}_{\Sigma} \rightarrow \mathcal{H}_{\Sigma^{\prime}}\quad \quad (2.36)$

图3：在带边界$\Sigma$和$\Sigma^\prime$的时空$M$上的路径积分，会定义一个跃迁振幅$\Phi_M: \mathcal{H}_\Sigma \to \mathcal{H}_{\Sigma^\prime}$。

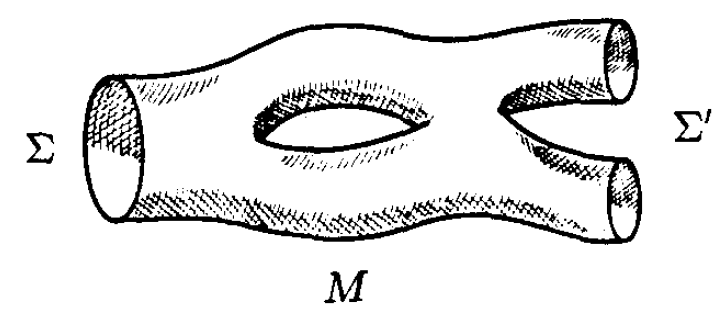
因子化现在就是这样的性质：如果将 $M$ 沿一个中间切片 $\Sigma''$ 切成 $M_1,M_2$ 两份，那么跃迁振幅满足

$\Phi_{M}=\Phi_{M_{2}} \circ \Phi_{M_{1}}\quad \quad (2.37)$

，如图4。因为我们复合的是线性算符，这个操作包含对中间Hilbert空间 $\mathcal{H}_{\Sigma''}$ 中态的求和。

图4：因子化公理要求，如果时空$M$被切成$M_1,M_2$两份，那么相应的跃迁振幅可复合：$\Phi_M=\Phi_{M_2}\circ \Phi_{M_1}$。

需要强调的是，这样的因子化是“物质理论”的特点。引力理论包含对所有度规的积分，不太一样：对度规的路径积分总会包含奇异的度规，这时流形的拓扑会退化。 $M$ 的拓扑因而不是良定义的，这里天真地假定的因子化不再成立。第4节再继续说。

2.6 二维中的拓扑场论

这里我们将考察限制在二维。时空成了世界面，取成一个亏格为 $g$ 的Riemann面 $\Sigma$ 。这样，我们求解理论的能力会大幅增强。

现在为二维拓扑场论构造算符代数。从物理Hilbert空间 $\mathcal{H}_{物理}$ 的一组完备基 $\{\phi_i\}$ 开始，我们可用两点函数在 $\mathcal{H}_{物理}$ 中定义非退化（但未必正）的度规 $\eta_{ij}$ ：

$\left\langle\phi_{i} \phi_{j}\right\rangle_{0}=\eta_{i j}\quad \quad (2.38)$

我们有通常的封闭关系

$\mathbf{1}_{物理}=\sum_{i, j}\left|\phi_{i}\right\rangle \eta^{i j}\left\langle\phi_{j}\right|\quad \quad (2.39)$

这里 $\eta^{ij}=\eta_{ij}^{-1}$ 用于升指标。

图5：二维曲面两种可能的因子化：沿平凡的同调闭链(a)，沿非平凡的同调闭链(b)。

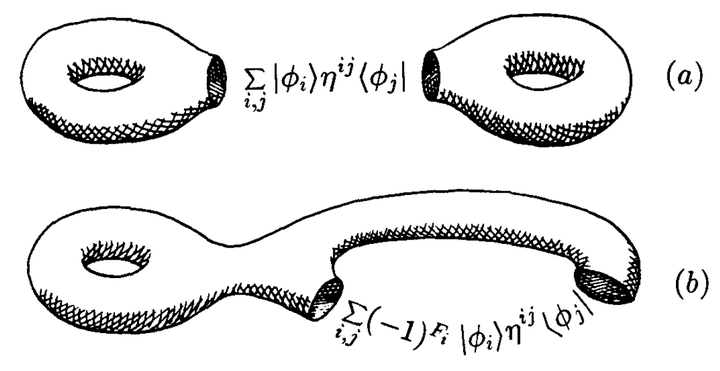
因子化的形式通过将 $\mathbf{1}_{物理}$ 插进关联函数来确定。几何上看，这是将Riemann面中的一个柱换成令场沿柱演化的酉算符。Hamiltonian为零，因此没有时间演化，结果因而不依赖于柱的长度。这与关联函数不依赖于度规一致。因子化的形式只取决于时空切口的类型，如图5。特别地，取决于切口的同伦类。切口可能绕着曲面的柄，也可能不绕着。如果切口不绕着柄（平凡同调），亏格为 $g$ 的曲面就被切成亏格为 $g'$ 和 $g-g'$ 的两份。有些算符（假定是其中的 $r$ 个）在第一份上，其余在另一份上。得到的 $s$ 点函数因子化公式是

$\left\langle\phi_{i_{1}} \phi_{i_{2}} \ldots \phi_{i_{s}}\right\rangle_{g}=\sum_{j, k}\left\langle\phi_{i_{1}} \ldots \phi_{i_{r}} \phi_{j}\right\rangle_{g^{\prime}} \eta^{j k}\left\langle\phi_{k} \phi_{i_{r+1}} \ldots \phi_{i_{s}}\right\rangle_{g-g^{\prime}}\quad \quad (2.40)$

这里，我们用了态 $|\phi_k\rangle$ 即插入算符 $\phi_k$ 。如果切口绕着柄（非平凡同调），曲面的亏格就减小1。这时 $s$ 点函数的因子化公式是

$\left\langle\phi_{i_{1}} \cdots \phi_{i_{s}}\right\rangle_{g}=\sum_{j, k} \eta^{j k}(-1)^{F_{j}}\left\langle\phi_{j} \phi_{k} \phi_{i_{1}} \cdots \phi_{i_{s}}\right\rangle_{g-1}\quad \quad (2.41)$

这里 $F_j$ 是场 $\phi_j$ 的费米数。（对易则 $F=0$ ，反对易则 $F=1$ 。）这样的关联函数因子化，加上不依赖于度规，给出了二维拓扑场论的基本框架。

因子化公式容许我们将更高亏格的关联函数切成亏格为零的。事实上，任意关联函数都可因子化成球面上的三点函数。这些因子记作

$c_{i j k}=\left\langle\phi_{i} \phi_{j} \phi_{k}\right\rangle_{0}\quad \quad (2.42)$

现在展示， $c_{ijk}$ 可组成结合代数。要点是四点函数间的对偶。由因子化公式 $(2.40)$ ，球面上的四点函数是

$\begin{aligned} \left\langle\phi_{i} \phi_{j} \phi_{k} \phi_{l}\right\rangle_{0} &=\sum_{m, n}\left\langle\phi_{i} \phi_{j} \phi_{m}\right\rangle_{0} \eta^{m n}\left\langle\phi_{n} \phi_{k} \phi_{l}\right\rangle_{0} \\ &=\sum_{m} c_{i j}{}^{m} c_{m k l} \end{aligned}\quad \quad (2.43)$

图6：球面上四点函数$\langle \phi_i \phi_j \phi_k \phi_l \rangle$间的对偶给出算符乘积代数的结合律。

可以因子化成 $s$ -道，也可以是 $t$ -道，如图6。结果应当是一样的，这就给出了很强的一致性条件

$\begin{aligned} \left\langle\phi_{i} \phi_{j} \phi_{k} \phi_{l}\right\rangle_{0}=\sum_{m} c_{i j}{}^{m} c_{m k l} &=\sum_{m} c_{i k}{}^{m} c_{m j l} \quad \quad (2.44)\\ s \text {-道} \ \ \ \ & \ \ \ \ \ \ \ \ \ \ \ \ t \text {-道} \end{aligned}$

，保证了代数有结合律。有了这点，这样用系数 $c_{ijk}$ 来表述算符代数就是有意义的：

$\phi_{i} \times \phi_{j}=\sum_{k} c_{i j}{}^{k} \phi_{k}\quad \quad (2.45)$

注意，度规是 $\eta_{ij}=c_{0ij}$ 。

图7：算符$H=\sum_{i,j} c_i {}^{ij} \phi_j$在曲面$\Sigma$上产生一个柄。

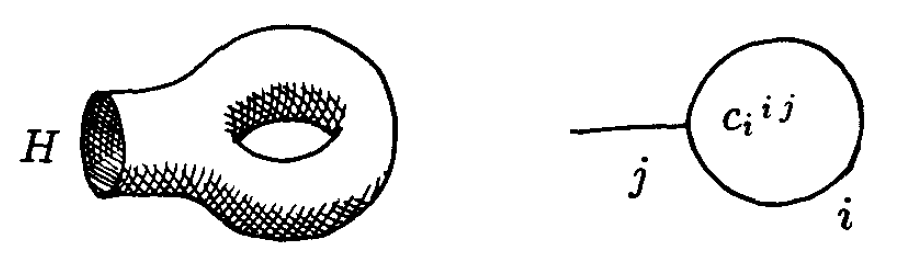
有了因子化的概念，计算更高亏格的配分函数和关联函数就特别简单。事实上，可以引入产生柄的算符 $H$ ^[4]。通过对应单孔环面的态来定义它，如图7：

$H=\sum_{i,j} c_i {}^{ij} \phi_j\quad \quad (2.46)$

这样，亏格为 $g$ 的配分函数 $Z_g$ 就可写成亏格为零的关联函数

$Z_{g}=\langle\underbrace{H \cdots H}_{g}\rangle_{0}\quad \quad (2.47)$

由此立刻知道，因子化公理成立的拓扑场论中，配分函数在亏格很大时多项式增长：

$Z_{g} \sim c^{g}\quad \quad (2.48)$

$c$ 是某个常数。这与二维量子引力和弦论中的结果截然不同，那里配分函数与模空间体积有关，表现出著名的双阶乘增长^[21]：

$Z_{g} \sim(2 g) !\quad \quad (2.49)$

这已经向我们表明，本节和下节考察的广义协变性最简单的类型，与引力理论不相关。必须作些适当的改动——放弃因子化——第4和5节再继续说。

2.7 非局域算符

现在考虑非局域算符。在二维是1-形式和2-形式算符的积分， $\int_{C} \phi^{(1)}$ 和 $\int_{\Sigma} \phi^{(2)}$ ， $C$ 是曲面 $\Sigma$ 上的非平凡闭链。1-形式算符不很有趣（之后会评论），但2-形式算符很关键。我们已经说过，它可加进Lagrangian，用局域密度 $\phi^{(2)}$ 对原来的理论作微扰。这给出新的作用量

$S(t)=S-\sum_{n} t_{n} \int d^{2} z \phi_{n}^{(2)}(z, \bar{z})\quad \quad (2.50)$

之后将在积分中略去 $\phi^{(2)}$ 的上标，因为只有2-形式才可积分。除非特别说明，积分是在整个世界面上作的。

如果我们知道了任意拓扑的曲面上，局域和2-形式算符的所有关联函数，就解出了二维拓扑场论。对局域算符，我们已经看到，它们的关联函数完全编码在三点函数 $c_{ijk}$ 中。一旦意识到微扰的模型 $(2.50)$ 仍定义了满足重要的因子化公理的拓扑理论，加上2-形式算符也是相当直接的。原来理论的所有代数结构在微扰后仍然保持。这促使我们将关联函数看成耦合常数 $t_n$ 的函数：

$\left\langle\phi_{i_{1}} \phi_{i_{2}} \ldots \phi_{i_{s}}\right\rangle_{g}(t) \equiv\left\langle\phi_{i_{1}} \phi_{i_{2}} \ldots \phi_{i_{s}} \exp \left(\sum_{n} t_{n} \int \phi_{n}\right)\right\rangle_{g}\quad \quad (2.51)$

$t=0$ 时回到原来的理论。作偏导就可得到包含2-形式算符积分的关联函数：

$\left\langle\phi_{i_{1}} \ldots \phi_{i_{s}} \int \phi_{j_{1}} \ldots \int \phi_{j_{r}}\right\rangle_{g}=\left.\frac{\partial}{\partial t_{j_{1}}} \ldots \frac{\partial}{\partial t_{j_{r}}}\left\langle\phi_{i_{1}} \phi_{i_{2}} \ldots \phi_{i_{s}}\right\rangle_{g}\right|_{t=0}\quad \quad (2.52)$

（这里是将耦合常数设成零，当然也可设成某个背景值 $t_n=\bar{t}_n$ 。）微扰的关联函数 $(2.51)$ 仍可因子化成三点函数

$c_{i j k}(t)=\left\langle\phi_{i} \phi_{j} \phi_{k} \exp \left(\sum_{n} t_{n} \int \phi_{n}\right)\right\rangle_{0}\quad \quad (2.53)$

这些三点函数现在也依赖于耦合常数 $t_n$ 。这样就很容易计算插入算符积分的关联函数。例如，插入一个2-形式算符积分的四点函数可因子化成

$\begin{aligned} \left\langle\phi_{i} \phi_{j} \phi_{k} \phi_{l} \int \phi_{n}\right\rangle_{0} &=\frac{\partial}{\partial t_{n}} \sum_{m} c_{i j}{}^{m} c_{m k l} \\ &=\sum_{m}\left(c_{i j}{}^{m}{}_{,n} c_{m k l}+c_{i j}{}^{m} c_{m k l, n}-c_{i j}{}^{m} c_{k l}{}^{p} \eta_{m p, n}\right) \end{aligned}\quad \quad ( 2.54)$

这里用了记号

$\begin{aligned} c_{i j k, n} &=\frac{\partial c_{i j k}}{\partial t_{n}}=\left\langle\phi_{i} \phi_{j} \phi_{k} \int \phi_{n}\right\rangle_{0} \\ \eta_{i j, n} &=\frac{\partial \eta_{i j}}{\partial t_{n}}=\left\langle\phi_{i} \phi_{j} \int \phi_{n}\right\rangle_{0} \end{aligned}\quad \quad (2.55)$

因子化 $(2.54)$ 也可通过仔细考虑不同区域积分的贡献推出。前两项是积分 $\int \phi_{n}$ 在切片两侧的贡献，第三项则是在无穷接近切片的区域。

总结一下：二维拓扑场论可完全用三点函数 $c_{ijk}$ 表述，这定义了物理算符 $\phi_i$ 的结合代数。此外，由于2-形式算符的存在，这些三点函数可看成一组形变参数 $t_i$ （对每个独立的物理场有一个）的，保持结合律的函数 $c_{ijk}(t)$ 。

3. 拓扑共形场论

我们已经看到，一般的二维拓扑场论可完全解出，得到用微扰三点函数 $c_{ijk}(t)$ 表述的代数。现在的目标是，对一系列与量子引力研究相关的例子，计算这些量。这需要引入些额外的结构：我们要求拓扑场论是共形不变的。这看起来有些不必要，因为拓扑场论中所有的物理量不依赖于度规，也就自动在共形变换下不变。然而，我们要求即使是非物理部分也共形不变。我们称这样的模型是拓扑共形场论（TCFT）。

3.1 扭 $\mathcal{N}=2$ 超共形模型

这种强的共形不变性，要求能动张量就是无迹：

$T_{\mu}{}^{\mu}=0\quad \quad (3.1)$

不只是在物理的关联函数中。能动张量仍有 $Q$ 伙伴 $G_{\mu\nu}$ ：

$T_{\mu \nu}=\left\{Q, G_{\mu \nu}\right\}\quad \quad (3.2)$

它也是无迹的。共形不变性容许我们选取共形规范 $g_{\mu \nu}=e^{\phi} \delta_{\mu \nu}$ ，用复坐标 $z,\bar{z}$ 。最终，我们会需要处理这规范在更高亏格遇到的拓扑障碍，但暂时只关注球面，这时可以在全局选取这规范。

拓扑共形场论具有两种根本的对称性：标度不变性和 $Q$ 对称性。由于共形不变性，这些对称性的生成元可分成正反全纯部分。能动张量分成全纯的 $T(z) \equiv T_{z z}$ 和反全纯的 $\bar{T}(\bar{z}) \equiv T_{\bar{z}\bar{z}}$ ，它的伙伴 $G_{\mu\nu}$ 也类似地分成 $G(z)$ 和 $\bar{G}(\bar{z})$ 。荷 $Q$ 将是左行的 $Q_L$ 和右行的 $Q_R$ 之和。 $Q_L$ 对应一个自旋1守恒流 $Q(z)$ ，“BRST流”。因为这场有非零的共形维数（其实就是能量） $h=1$ ，根据2.4节的一般论证，必然是 $Q$ -恰当的。于是，它有一个同样是自旋1的玻色伙伴 $J(z)$ ：

$Q(z)=\{Q, J(z)\}\quad \quad (3.3)$

注意， $J(z)$ 是常规的 $U(1)$ 流。所有场 $\phi_i$ 可选成具有确定的（左，右）共形维数 $(h_i,\bar{h}_i)$ ，以及关于这 $U(1)$ 对称性的荷 $(q_i,\bar{q}_i)$ 。

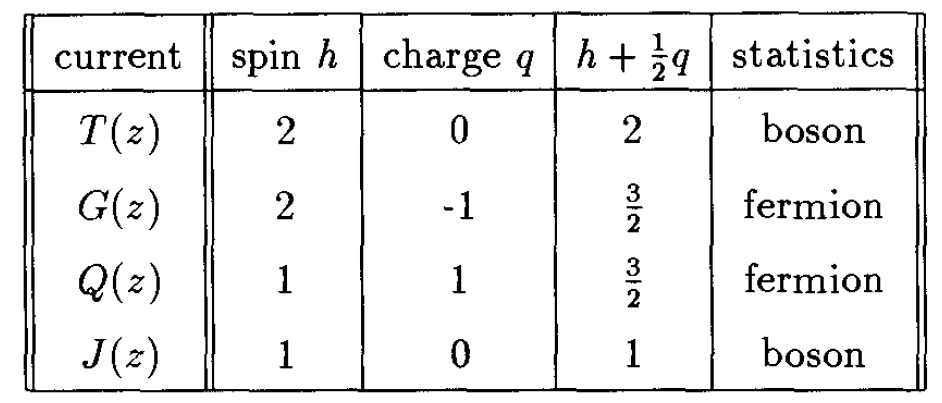
因此我们得到了列在表1中的流多重态。这多重态当然非常像标准的流 $\mathcal{N}=2$ 超多重态，但自旋不对。技巧就是像上节解释的那样，扭一下理论以得到同超对称一致的自旋。事实上，如果将共形维数换成 $h+q/2$ ，流 $Q(z)$ 和 $G(z)$ 就获得自旋3/2。因此正确的扭操作是

$T \rightarrow T_{\mathcal{N}=2}=T-\frac{1}{2} \partial J, \quad h \rightarrow h_{\mathcal{N}=2}=h+\frac{1}{2} q \quad \quad (3.4)$

现在考虑四个流 $T,G,Q,J$ 生成的代数。如果它们构成封闭代数——当然不一定是这样——它们的算符乘积就完全固定下来了。这是因为扭后会得到 $\mathcal{N}=2$ 超共形代数，而它是唯一的。那么就得到如下的算符乘积：

$\begin{aligned} &T(z) T(w) \sim \frac{2 T}{(z-w)^{2}}+\frac{\partial T}{z-w}, \quad \quad J(z) J(w) \sim \frac{d}{(z-w)^{2}} \\& T(z) Q(w) \sim \frac{Q}{(z-w)^{2}}+\frac{\partial Q}{z-w}, \quad \quad J(w) Q(z) \sim \frac{Q}{z-w} \\& T(z) G(w) \sim \frac{2 G}{(z-w)^{2}}+\frac{\partial G}{z-w}, \quad \quad J(z) G(w) \sim \frac{-G}{z-w} \\& T(z) J(w) \sim \frac{-d}{(z-w)^{3}}+\frac{J}{(z-w)^{2}}+\frac{\partial J}{z-w}\\ &Q(z) G(w) \sim \frac{d}{(z-w)^{3}}+\frac{J}{(z-w)^{2}}+\frac{T}{z-w}\\ &G(z) G(w) \sim Q(z) Q(w) \sim 0 \end{aligned}\quad \quad (3.5)$

其中多数都是含义自明的：就是表达流的共形维数和荷。要注意的是出现了 $U(1)$ 对称性的中心荷 $d$ 。在sigma模型的情形，它对应目标空间的维数，这正是我们记作 $d$ 的原因。能动张量与 $U(1)$ 流算符乘积的反常中也出现了这个常数，之后再回到这点。可能在第一条方程中出现的共形中心荷，在这里为零，因为广义协变的理论不容许共形反常（可与临界弦比较）。拓扑模型中的 $U(1)$ 反常，与相应超对称理论的中心荷间的关系是 $c=3d$ 。

$U(1)$ 流 $J(z)$ 的反常给出关联函数的选择规则。从 $(3.5)$ 中 $T$ 与 $J$ 的算符乘积可以直接看到， $J(z)$ 在坐标变换下的行为并非常规的。令 $w(z)$ 是全纯坐标变换，那么

$\oint d w J(w)=\oint d z J(z)+d \cdot \oint \partial_{z}\left(\log \partial_{z} w\right)\quad \quad (3.6)$

因此，在反演 $w=1/z$ 下，零模 $J_0$ 成了 $J_0-d$ ，我们得到球面上有背景荷 $-d$ 。任意拓扑的背景荷可从 $U(1)$ 反常的协变表达式

$\nabla_{\mu} J^{\mu}=\frac{d}{8 \pi} \sqrt{g} R\quad \quad (3.7)$

求出， $g_{\mu\nu}$ 是世界面度规， $R$ 是标量曲率。那么，因为曲率密度积分给出Euler示性数，对亏格为 $g$ 的曲面是 $\chi=2g-2$ ，就有了需要抵消的背景荷 $d\cdot (g-1)$ ，关联函数要满足选择规则

$\left\langle\phi_{i_{1}} \ldots \phi_{i_{s}}\right\rangle_{g} \neq 0 \longrightarrow \sum q_{i}=d(1-g)\quad \quad (3.8)$

此外注意，2-形式算符

$\phi_{i}^{(2)}=G_{-1} \bar{G}_{-1} \phi_{i}^{(0)}\quad \quad (3.9)$

带（左，右）荷 $(q_i-1,\bar{q}_i-1)$ 。

通过上面的扭操作，任意 $\mathcal{N}=2$ 超共形模型都可给出拓扑共形场论。这不只是提供了丰富的例子，在 $\mathcal{N}=2$ 超对称语境下还可由此推出些有趣的结果。 $\mathcal{N}=2$ 模型中有一个自然的内积，我们可沿用到拓扑场论中。根据这内积，我们有Hermite性质 $Q^\dagger=G_0$ 。在2.4节我们已经看到，借助这点可证明物理态满足

$Q|\phi\rangle=0, \quad G_{0}|\phi\rangle=0 \quad \quad (3.10)$

后一个条件在每个 $Q$ -上同调类中选出了唯一的代表元。这可与常规上同调理论中的调和形式比较。在 $\mathcal{N}=2$ 语境下，这些场是手征初级场^[22]。

3.2 广义 $SL(2,\mathbb{C})$ 不变性及其推论

TCFT关联函数也可用超场写， $(2.17)$ 在这里是

$\Phi(z, \bar{z}, \theta, \bar{\theta})=\phi^{(0)}(z, \bar{z})+\phi^{(1)}(z, \bar{z}) \theta+\bar{\phi}^{(1)}(z, \bar{z}) \bar{\theta}+\phi^{(2)}(z, \bar{z}) \theta \bar{\theta}\quad \quad (3.11)$

有趣的关联函数形如

$\left\langle\prod_{i=1}^{s} \int d^{2} z d^{2} \theta \Phi_{i}(z, \bar{z}, \theta, \bar{\theta})\right\rangle_{g}\quad \quad (3.12)$

然而，这些关联函数在球面上不是良定义的。物理场在算符 $L_0,L_1,L_{-1}$ 和 $G_0,G_1,G_{-1}$ 生成的 $SL(2,\mathbb{C})$ 对称性的费米扩张下不变。这些对称性对应超Möbius变换

$z \rightarrow \tilde{z}=\frac{a z+b}{c z+d}, \quad \theta \rightarrow \tilde{\theta}=\frac{\theta+\alpha z^{2}+\beta z+\gamma}{(c z+d)^{2}}\quad \quad (3.13)$

$SL(2,\mathbb{C})$ 对称性可将三个 $z$ 坐标固定在 $0,1,\infty$ ，将三个 $\theta$ 坐标固定在 $0$ 。回忆一下

$\int d^{2} \theta \Phi=\phi^{(2)}, \quad \left.\quad \Phi\right|_{\theta=0}=\phi^{(0)}\quad \quad (3.14)$

就知道上面的关联函数可换成

$\left\langle\phi_{i_{1}}^{(0)} \phi_{i_{2}}^{(0)} \phi_{i_{3}}^{(0)} \int \phi_{i_{4}}^{(2)} \ldots \int \phi_{i_{s}}^{(2)}\right\rangle_{g=0}\quad \quad (3.15)$

因为我们是从关于所有指标 $i_k$ 对称的表达式开始的，这个关联函数就也有这对称性。也就是说，具体将哪三个算符取成0-形式无关紧要。这个广义的 $SL(2,\mathbb{C})$ 不变性告诉我们，0-形式和2-形式可以互换位置。用系数 $c_{ijk}(t)$ 写，这就给出可积条件

$\frac{\partial c_{i j k}}{\partial t_{l}}=\frac{\partial c_{i j l}}{\partial t_{k}}\quad \quad (3.16)$

我们可以积分这条件三次，得到三点函数其实就是一个函数 $F(t)$ ，所谓的自由能的三阶导：

$c_{i j k}(t)=\frac{\partial^{3} F(t)}{\partial t_{i} \partial t_{j} \partial t_{k}}\quad \quad (3.17)$

$F(t)$ 形式上定义成

$F(t)=\left\langle\exp \left(\sum_{n} t_{n} \int \Phi_{n}\right)\right\rangle\quad \quad (3.18)$

现在考虑特殊的恒等算符 $\phi_0=\textbf{1}$ 。因为 $G$ 与恒等算符对易，没有对应的2-形式，也就不存在耦合常数 $t_0$ 。这点加上可积关系 $(3.16)$ ，得到

$0=\frac{\partial c_{i j k}}{\partial t_{0}}=\frac{\partial c_{i j 0}}{\partial t_{k}}=\frac{\partial \eta_{i j}}{\partial t_{k}}\quad \quad (3.19)$

因此我们证明了，度规或者说两点函数 $\eta_{ij}$ 不依赖于形变参数 $t_k$ 。[这个论证的一个手征版本表明，形如

$\left\langle\phi_{i} \phi_{j} \oint \phi_{k}^{(1)}\right\rangle_{0}\quad \quad (3.20)$

的关联函数也为零。再由因子化可知，只要不相交，回路积分的关联函数就为零。]

总结一下，对拓扑共形场论的特例，我们推出了三个重要结果。第一，所有系数 $c_{ijk}(t)$ 可由单个函数，自由能 $F(t)$ 得到。第二，态的Hilbert空间中的度规 $\eta_{ij}(t)$ 不依赖于耦合常数 $t_k$ 。第三，存在一个反常的 $U(1)$ 对称性，这可翻译成自由能的标度关系

$\sum_{j}\left(q_{j}-1\right) t_{j} \frac{\partial}{\partial t_{j}} F(t)=(d-3) F(t)\quad \quad (3.21)$

值得指出的是，有这三个就足够解出许多特例了，特别是所有 $d<1$ 的模型^[12]。

3.3 拓扑共形场论的例子

现在考虑一些TCFT的例子会有所帮助。这些例子旨在解释，为什么上面的构造中强调了一些特定结构，并提供改动更高亏格关联函数的动机，这是下节将讨论的。

第一个例子是两玻色子和两费米子的自由场论。这是最简单的，也会令读者确信上面的讨论并不空洞。玻色子属于一个复二重态 $x(z,\bar{z})$ 和 $\bar{x}(z,\bar{z})$ 。它们由通常的自由玻色Lagrangian

$\mathcal{L}_{B}=\partial \bar{x} \bar{\partial} x\quad \quad (3.22)$

描述，中心荷 $c_B=2$ 。费米子被选成抵消这个中心荷，它们的Lagrangian是

$\mathcal{L}_{F}=\chi \bar{\partial} \psi+\bar{\chi} \partial \bar{\psi}\quad \quad (3.23)$

$\psi$ 的自旋是0，带荷1， $\chi$ 的自旋是1，带荷-1，给出需要的中心荷 $c_F=-2$ 。下一步是找到幂零的荷 $Q$ 。它应当对应变换（未写出的不变）

$\begin{array}{ll} \delta x=\psi, & \bar{\delta} \bar{x}=\bar{\psi} \\ \delta \chi=\partial \bar{x}, & \bar{\delta} \bar{\chi}=\bar{\partial} x \end{array}\quad \quad (3.24)$

这里， $\delta$ 代表左行荷 $Q_L$ 对场的作用：

$\delta=\left\{Q_{L}, \cdot\right\}\quad \quad (3.25)$

类似地， $\bar{\delta}=\left\{Q_{R}, \cdot\right\}$ 。比对Lagrangian $(3.22),(3.23)$ 和场变换 $(3.24)$ ，可以看到重要的性质：总Lagrangian是 $Q$ -恰当的：

$\mathcal{L}=\{Q, \chi \bar{\partial} x+\bar{\chi} \partial \bar{x}\}\quad \quad (3.26)$

能动张量也是：

$T=\partial \bar{x} \partial x+\chi \partial \psi=\{Q, \chi \partial x\}\quad \quad (3.27)$

现在可以知道左行荷是

$Q_{L}=\oint \psi \partial \bar{x}=\oint\{Q, \psi \chi\}\quad \quad (3.28)$

总结一下，这个例子中的流是

$\begin{aligned} T(z) &=\partial \bar{x} \partial x+\chi \partial \psi \\ Q(z) &=\psi \partial \bar{x} \\ J(z) &=\psi \chi \\ G(z) &=\chi \partial x \end{aligned}\quad \quad (3.29)$

这个模型就是 $\mathcal{N}=2$ 代数的标准 $c=3$ 自由场实现扭出来的，描述由坐标 $x,\bar{x}$ 参数化的时空中运动的弦。物理态是

$\{1, \psi, \bar{\psi}, \psi \bar{\psi}\}\quad \quad (3.30)$

算符 $x$ 虽然不恰当，但由于红外奇点，不产生态。

上面的自由场论可朝两个方向作有趣的推广。第一，我们可以考虑非线性sigma模型，将平坦的复一维时空换成任意的 $d$ 维Ricci-平坦的Kähler流形 $M$ 。用超场写，作用量是

$S=\int d^2 zd^2\theta K(X^i,X^{\bar{i}})\quad \quad (3.31)$

$K$ 是Kähler势， $X^i,X^{\bar{i}}$ （ $i=1,...,d$ ）是 $M$ 上的局域坐标。这些模型具有 $\mathcal{N}=2$ 超共形不变性，扭后就有拓扑不变性。

第二是加上超势，也就是如下形式的作用量：

$S=\int d^{2} z d^{2} \theta K\left(X^{i}, X^{\bar{i}}\right)+\int d^{2} z d^{2} \theta W\left(X^{i}\right)+c . c .\quad \quad(3.32)$

如果超势 $W(X^i)$ 是准齐次的，那么在重整化群的不动点处，这些Landau-Ginzburg模型是共形不变的^[23]^[24]。准齐次就是说，对荷 $q_i$ ，有标度律

$W(\lambda^{q_i}X^i)=\lambda W(X^i)\quad \quad (3.33)$

这时，拓扑模式的所有动力学被超势的形式完全固定住。最简单的例子中，有一个场 $X=x+...$ ，势是

$W(X)=X^{n} \quad \quad (3.34)$

相当惊人的是，当我们在第5节深入讨论与矩阵模型的关联时，会出现这个模型。

3.4 临界弦论

拓扑共形场论的最后一个例子，可能有些惊人，是已经过时的26维临界玻色弦论。众所周知，这个理论分成物质和鬼的部分，这反映在能动张量中：

$T=T^{\text {物质}}+T^{\text {鬼}}\quad \quad (3.35)$

总的中心荷为零。为固定住重参数化不变性容许的规范，加入鬼 $c$ 和反鬼 $b$ 是必要的。它们的共形自旋分别是2和-1，能动张量是 $T^{\text {鬼}}=2 \partial c b+c \partial b$ 。幂零的荷 $Q$ 在这里确实是BRST荷：

$Q=\oint: c\left(T^{物质}+\frac{1}{2} T^{鬼}\right):\quad \quad (3.36)$

我们可以再次看到，能动张量和BRST流 $Q(z)$ 是 $Q$ -恰当的：

$\begin{array}{ll} T(z)=\{Q, b(z)\} &\longrightarrow G(z)=b(z) \\ Q(z)=\{Q, b c(z)\} &\longrightarrow J(z)=b c(z) \end{array}\quad \quad (3.37)$

这里用了 $\{Q, c\}=c \partial c$ 。 $U(1)$ 背景荷（鬼荷）在这里是 $-d=-3$ 。仔细的考察表明，这里的代数不是封闭的。事实上，生成了流 $c(z)$ 和 $c\partial c(z)$ ，得到封闭代数要把它们加进去。

这里的0-形式和2-形式大家也都熟悉。它们由共形维数为 $(1,1)$ 的物理顶点算符 $V(z,\bar{z})$ 生成：

$\phi^{(0)}=c \bar{c} V, \quad \phi^{(2)}=V=b_{-1} \bar{b}_{-1} \phi^{(0)}\quad \quad (3.38)$

这时， $U(1)$ 选择规则强力限制住了这些算符的关联函数。需要抵消掉球面上的背景荷-3，而 $(3.38)$ 中算符的荷，分别是 $q=1$ 和 $q=0$ ，那么唯一的非零关联函数形如

$\left\langle\phi_{i_{1}} \phi_{i_{2}} \phi_{i_{3}} \int \phi_{j_{1}} \ldots \int \phi_{j_{r}}\right\rangle_{0} \quad \quad (3.39)$

这就是弦论中通常考虑的树图阶关联函数。更高亏格时，这些关联函数为零，因为不再满足选择规则 $\sum q_{n}=3(1-g)$ 。解决方法是加入不BRST闭的场。关联函数因而依赖于Riemann面的模空间——不再是拓扑的——应当在模空间中积分，留下只依赖于曲面亏格的拓扑表达式。这样我们回到了Polyakov方法。

更具体地说，我们有计算关联函数的如下规则：考虑亏格为 $g$ Riemann面的模空间 $\mathcal{M}_g$ ，局域坐标记作 $m_a,\bar{m}_a$ 。选取与 $\mathcal{M}_g$ 相切的向量 $\mu_a,\bar{\mu}_a$ ——Beltrami微分。考虑如下形式的关联函数：

$\left\langle\phi_{i_{1}} \cdots \phi_{i_{r}}\right\rangle_{g} \equiv \int_{\mathcal{M}_{g}} \prod d^{2} m_{a}\left\langle\int \phi_{i_{1}} \cdots \int \phi_{i_{r}} \prod_{a=1}^{3 g-3} \int_{\Sigma} \mu_{a} b \int_{\Sigma} \bar{\mu}_{a} \bar{b}\right\rangle_{g}\quad \quad (3.40)$

因子 $\int \mu_{a} b=\int \mu_{a} G$ 确保了模不变性。因为反鬼 $b(z)$ 带荷-1，我们插入 $3g-3$ 个以抵消背景荷，刚好足以使得被积函数成为模空间中的体积形式。这样定义就与拓扑不变性一致。非物理的算符解耦，这是因为能动张量和Beltrami微分放在一起，给出模空间中的全导数：形如

$\left\langle\phi_{i_{1}} \cdots \phi_{i_{r}}\{Q, \lambda\}\right\rangle\quad \quad (3.41)$

的关联函数包含如下贡献：

$\left\{Q, \int_{\Sigma} \mu_{a} b\right\}=\int \mu_{a}\{Q, b\}=\int \mu_{a} T=\frac{\partial S}{\partial m_{a}}\quad \quad (3.42)$

因为模空间是紧的，这全导数积分天真看来为零。可以看到，对改动的关联函数，选择规则就是

$\sum q_{n}=0\quad \quad (3.43)$

因为插入反鬼已经贡献了 $3-3g$ 。这说明，虽然天真看来为零，关联函数也可在更高亏格定义。不过有些微妙之处。上面的构造高度依赖于，背景荷刚好是 $-d=-3$ ，且所有（局域）算符带 $q=1$ 。这种方法可推广到任意拓扑场论，自然促使我们考察拓扑引力和拓扑弦论，这是下节的主题。

4. 拓扑弦论

现在开始讨论拓扑引力与拓扑弦论。和传统弦论一样，拓扑弦包含与Liouville和鬼场耦合的物质理论。物质部分就是上节讨论的拓扑共形场论。我们已经看到，存在幂零的荷 $Q$ 将大幅简化问题。我们的目标是引入一个动力学度规，规范固定后相当于引入一个Liouville型场和鬼，同时保持 $Q$ 对称性。讲解时基本照着E. 和H. Verlinde的工作^[7]^[16]。我们从最简单的例子开始解释构造。

4.1 作用量和对称性

我们来重新考察3.3节提到的 $d=1$ 拓扑sigma模型，现在对一般的世界面度规写，它的Lagrangian是

$\mathcal{L}=\sqrt{g} g^{\mu \nu}\left\{\partial_{\mu} x \partial_{\nu} \bar{x}+\chi_{\mu} \partial_{\nu} \psi\right\}\quad \quad (4.1)$

我们想令这个模型与引力耦合，这样度规 $g_{\mu\nu}$ 成为动力学的，同时不破坏 $Q$ 对称性确保的拓扑不变性。那么，每个场都要有费米伴子。于是，我们引入度规的费米伴子 $\psi_{\mu\nu}$ 以及变换规则

$\delta g_{\mu \nu}=\psi_{\mu \nu}, \quad \delta \psi_{\mu \nu}=0 \quad \quad (4.2)$

就像关于度规变分作用量给出能动张量一样，关于 $\psi_{\mu\nu}$ 变分将给出它的伙伴 $G_{\mu\nu}$ ：

$T^{\mu \nu}=\frac{1}{\sqrt{g}} \frac{\delta S}{\delta g_{\mu \nu}}, \quad G^{\mu \nu}=\frac{1}{\sqrt{g}} \frac{\delta S}{\delta \psi_{\mu \nu}}\quad \quad (4.3)$

我们已经知道 $G_{\mu\nu}=\chi_\mu\partial_\nu x$ ，那么将泛函导数积分就得到完整的作用量

$\mathcal{L}=\sqrt{g} g^{\mu \nu}\left\{\partial_{\mu} x \partial_{\nu} \bar{x}+\chi_{\mu} \partial_{\nu} \psi+\psi_{\mu \rho} \chi^{\rho} \partial_{\nu} x\right\}\quad \quad (4.4)$

选取共形规范

$g_{\mu \nu}=e^{\phi} \delta_{\mu \nu}, \quad \psi_{\mu \nu}=\rho e^{\phi} \delta_{\mu \nu}\quad \quad (4.5)$

于是就要引入玻色（对易）鬼 $\beta,\gamma$ 和费米（反对易）鬼 $b,c$ 。鬼 $b,\beta$ 的自旋是2， $c,\gamma$ 的自旋是-1。总的中心荷当然还是零。对鬼系统写下生成元 $T,G,Q,J$ ，验证满足通常关系，是个简单的练习。

用共形因子 $\phi,\rho$ 写，度规的 $Q$ 变换是

$\delta\phi=\rho,\quad \delta \rho=0\quad \quad (4.6)$

因为总的中心荷为零，我们可用条件 $\partial \bar{\partial} \phi=\hat{R}$ 和 $\partial \bar{\partial} \rho=0$ 固定住移动这些模式的Weyl变换， $\hat{R}$ 是背景度规 $\hat{g}_{\mu\nu}$ 的世界面曲率。这些条件可借助Lagrange乘子 $\pi,\lambda$ 施加。那么理论总的作用量是

$\begin{aligned} &S=S_{物质}+S_{鬼}+S_{\text {Liouville}} \\& S_{鬼}=\int b \bar{\partial} c+\beta \bar{\partial} \gamma+c.c. \\& S_{\text {Liouville}}=\int \pi(\partial \bar{\partial} \phi-\hat{R})-\lambda \partial \bar{\partial} \rho \end{aligned}\quad \quad (4.7)$

我们提到过，所有这三个系统都有流多重态 $(T,G,Q,J)$ 。

为求出物理谱，必须知道正确的BRST荷。事实上，有两种选择。第一，我们有一个自带幂零的荷 $Q$ 的拓扑场论，这点被非常小心地保持了。第二，我们在处理一个规范理论，规范掉了能动张量 $T$ 和它的费米伙伴 $G$ 生成的对称性，那就有鬼和它的BRST荷。这BRST荷形如

$Q_{B R S T}=\oint: c\left(T_{物质}+T_{\text{Liouville}}+\frac{1}{2} T_{鬼}\right)+\gamma\left(G_{物质}+G_{\text{Liouville}}+\frac{1}{2} G_{鬼}\right):\quad \quad (4.8)$

这是熟知的玻色弦 $Q_{B R S T}$ 的简单推广。仔细的分析表明，这时上同调决定着理论谱的正确的BRST荷，是这两个荷之和：

$Q_{总}=Q+Q_{B R S T}\quad \quad (4.9)$

我们不会在这里重复的一段分析指出，关于 $Q_{总}$ 的物理算符形如 $\phi_{i} \cdot \sigma_{n}$ ， $\phi_i$ 是带荷 $q_i$ 的物质场， $\sigma_n$ （ $n=0,1,...$ ）是鬼和Liouville场的一个组合，带荷 $n$ ，这是个非负整数。这些引力场 $\sigma_n$ 是拓扑弦论的新特点，我们将仔细考察它们的性质。

现在必须说明如何计算这些算符的关联函数。和临界弦论一样，我们定义更高亏格的关联函数以使它们成为Riemann面模空间中体积形式的积分。具体的定义是

$\left\langle\mathcal{O}_{1} \ldots \mathcal{O}_{n}\right\rangle_{g} \equiv \int_{\mathcal{M}_{g}} \prod d^{2} m_{a}\left\langle\int \mathcal{O}_{1}^{(2)} \ldots \int \mathcal{O}_{n}^{(2)} \prod_{a=1}^{3 g-3} \int \mu_{a} G \int \bar{\mu}_{a} \bar{G}\right\rangle_{g}\quad \quad (4.10)$

选择规则是

$\sum_{k}\left(n_{k}+q_{i_{k}}-1\right)=(d-3)(1-g)\quad \quad (4.11)$

这些算符形如 $\mathcal{O}_{k} \equiv \phi_{i_{k}} \cdot \sigma_{n_{k}}$ 。关联函数 $(4.10)$ 是临界弦论中 $(3.40)$ 的推广。反鬼 $b(z)$ 换成了超流 $G(z)$ 。很快将看到，选择规则 $(4.11)$ 在矩阵模型中对应标度关系。这使我们能直接计算弦磁化率 $\gamma_{st}$ ，也就是算符的反常维数等。

4.2 纯拓扑引力

接着在纯拓扑引力，也就是没有物质的情形（ $d=0$ ），求解拓扑弦论。因为我们处理的是上同调理论，算符有很多可能的代表元。这里按^[7]，选取代表元以使模空间的内部不贡献关联函数。

我们从算符 $\sigma_n$ 的定义开始：

$\sigma_{n}=e^{\frac{2}{3}(n-1) \pi}(\tilde{\gamma})^{n}, \quad \tilde{\gamma}=\bar{\partial}\left(\frac{1}{2} \partial c+c \partial \phi-c.c.\right)\quad \quad (4.12)$

为直观些理解这个定义，我们引入 $Q=Q_{L}+Q_{R}$ 和 $Q_{-}=Q_{L}-Q_{R}$ 。回忆一下，这些算符可解释成世界面上的Dolbeault算符 $\partial,\bar{\partial}$ ，于是可以验证

$\tilde{\gamma}=\left\{Q,\left\{Q_{-}, \phi\right\}\right\} \sim \partial \bar{\partial} \phi=\hat{R}\quad \quad (4.13)$

因此 $\tilde{\gamma}$ 可解释成曲率，那么 $\sigma_n$ 对应 $\hat{R}$ 的 $n$ 次幂。注意， $\tilde{\gamma}$ 天真看来解耦，因为它是BRST恰当的。然而，这样模型还不是良定义的。为无歧义地定义关联函数，必须将场限制在“大”Hilbert空间 $\mathcal{H}$ 的一个子空间 $\mathcal{H}_0$ 中：

$\mathcal{H}_{0} \equiv\left\{|\phi\rangle \in \mathcal{H} \mid \left(L_{0}-\bar{L}_{0}\right)|\phi\rangle=\left(b_{0}-\bar{b}_{0}\right)|\phi\rangle=0\right\}\quad \quad (4.14)$

不然，在 $\mathcal{M}_{g,s}$ 中全局地定义关联函数会遇到障碍^[25]。因此，物理的Hilbert空间 $\mathcal{H}_0$ 由关于 $b_{0}-\bar{b}_{0}$ 等变的 $Q$ 上同调类构成。这确保了可在孔处一致地定义局域坐标。鬼 $c_0$ 不会被 $b_{0}-\bar{b}_{0}$ 湮灭，因此，虽然 $\tilde{\gamma}$ 在 $\mathcal{H}$ 中是BRST恰当的，但在 $\mathcal{H}_0$ 中不是，所以不解耦。

由于纯拓扑引力中 $d=0$ ，选择规则 $(4.11)$ 成为

$\left\langle\sigma_{n_{1}} \ldots \sigma_{n_{s}}\right\rangle_{g} \neq 0 \quad \longrightarrow \quad \sum_{i}\left(n_{i}-1\right)=3 g-3\quad \quad (4.15)$

4.3 接触和因子化项

关联函数 $(4.10)$ 包含亏格为 $g$ ，带 $s$ 个孔的曲面 $\Sigma_{g,s}$ 的模空间 $\mathcal{M}_{g,s}$ 中的积分。 $\mathcal{M}_{g,s}$ 的维数是

$\operatorname{dim} \mathcal{M}_{g, s}=3 g-3+s\quad \quad (4.16)$

这空间包含代表奇异曲面的点，也就是带退化度规的曲面。Polyakov特别强调过，这是引力理论相当一般的特征。度规的空间有边界，在边界上时空是奇异的。因此，在拓扑引力中也必须考虑边界 $\partial \mathcal{M}_{g,s}$ 。我们想为 $\mathcal{M}_{g,s}$ 加上额外的点，以使它紧。这应当同通常的 $\mathbb{R}^n$ 紧化作比较：在那种情形，我们加上无穷远点得到 $n$ -球面 $S^n$ 。在量子场论中自然出现的紧化是所谓的Deligne-Mumford紧化 $\overline{\mathcal{M}}_{g,s}$ ，它是从低维模空间归纳地构造的。

有两类退化的曲面需要考虑：可能是两孔重合，也可能是曲面变得奇异了。假定点 $x_2$ 接近点 $x_1$ 。由于共形对称性，极限情形并不只是标记了单个点的曲面。例如，可在某个局域坐标下将两点参数化成 $x_1=0$ 和 $x_2=qz,q\to 0$ 。然而，作全纯坐标变换 $y=x/q$ 后，我们发现两点的新坐标是 $y_1=0$ 和 $y_2=z$ ，距离保持不变。虽然点 $y_1$ 不会更接近 $y_2$ ，但它们确实被一个宽 $q$ 的细颈部同曲面的其余部分分开来了。 $q\to 0$ 时，这颈部被夹断了，留下由一结点连起来的两曲面。这说明，边界处的点代表一个标记了 $s-1$ 个点的曲面，加上标记了三个点的球面，如图8。这类退化可用符号写成

$\Sigma_{g, s} \to \Sigma_{g, s-1}+\Sigma_{0,3}\quad \quad (4.17)$

图8：如果两被标记的点互相接近，距离$q \to 0$，那么曲面退化。这共形等价于形成一个细长的颈部。在模空间的紧化中，最终的构型是一个标记了三个点的被夹断出去的球面，加上少了一个孔的原来的曲面。

因为带三个孔的球面模空间是零维的，我们在紧化中加入的子空间（复）余维数为1。这点从CFT的角度看相当自然。如果将两算符 $\phi_i(x_1),\phi_j(x_2)$ 放在一起，我们必须考虑它们的算符乘积

$\phi_i(x_1)\phi_j(x_2)\sim c_{ij}{}^k(x_1-x_2)^\Delta \phi_k(x_1)\quad \quad (4.18)$

$c_{ijk}=\langle \phi_i\phi_j\phi_k \rangle$ 是球面上的三点函数。

模空间的另一类边界由带奇异度规的曲面构成。当度规变得奇异，曲线的长度将变成零——这共形等价于形成一个长颈部——曲面以两种不同的方式被夹断，如图9。可以是被夹断成两不连通曲面，每个都被标记了一个额外的点——度规变得奇异的位置，这可用符号写成

$\Sigma_{g, s} \to \Sigma_{g^{\prime}, s^{\prime}+1}+\Sigma_{g-g^{\prime}, s-s^{\prime}+1}\quad \quad (4.19)$

也可以是一个柄退化掉，于是曲面的亏格减小1，被标记了两个额外的点：

$\Sigma_{g,s} \to \Sigma_{g-1,s+2}\quad \quad (4.20)$

图9：曲面退化的两种不同方式，平凡的同调闭链被夹断(a)，或非平凡的同调闭链被夹断(b)。图中展示了模空间的紧化中加入的曲面。

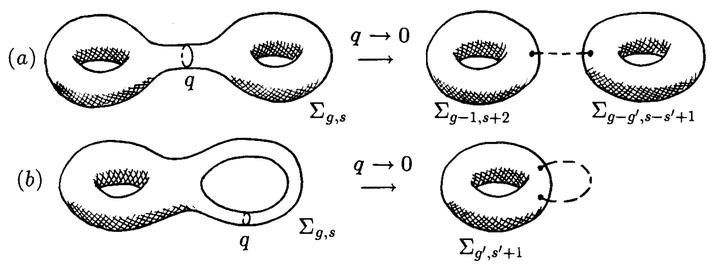
在这两种情形都很容易验证，加入的曲面模空间是低一维的。

^[7]中展示了，纯拓扑引力的关联函数由模空间的边界 $\partial \mathcal{M}_{g,s}$ 完全确定。事实上，有了两算符对撞时的接触项，就足够解出模型了。要看到这点，我们需要具体求出接触项代数。大概说一下^[7]中的论证。

定义态 $|\sigma_m\rangle=\sigma_m(0)|0\rangle$ ，考虑算符 $\sigma_n$ 在接近 $\sigma_m$ 时的贡献，它在某个坐标下位于 $z=0$ 处：

$\int d^{2} z \sigma_{n}(z, \bar{z}) \sigma_{m}(0)=\int_{|q|<\epsilon} \frac{d^{2} q}{|q|^{2}} G_{0} \bar{G}_{0} q^{L_{0}} \bar{q}^{\bar{L}_{0}} \sigma_{n}(1)\left|\sigma_{m}\right\rangle\quad \quad (4.21)$

就像上面说的，距离 $q$ 描述退化成结点的颈部。因子 $q^{L_{0}} \bar{q}^{\bar{L}_{0}}$ 描述沿颈部的演化。插入 $G_{0} \bar{G}_{0}$ 是为了确保模不变性，通过积掉 $q$ 的费米伴子得到。现在回忆一下， $\sigma_{n} \sim \tilde{\gamma}^{n}$ ， $\tilde{\gamma}=\left\{Q,\left\{Q_{-}, \phi\right\}\right\}$ 。因为 $L_0$ 是 $Q$ -恰当的，我们得到接触项中包含如下形式的贡献：

$\sim \int d^{2} q \partial_{q} \partial_{\bar{q}} q^{L_{0}} \bar{q}^{\bar{L}_{0}} \phi(0)\left|\sigma_{n+m-1}\right\rangle\quad \quad (4.22)$

这里 $q^{L_{0}} \bar{q}^{\bar{L}_{0}} \phi(0) \sim \log |q|^{2}+正规项$ ，因为场 $\phi$ 不是协变的。显然这给出 $\delta$ -函数，加上所有因子最终得到

$\int d^{2} z \sigma_{n}(z, \bar{z}) \sigma_{m}(0)=(m+\frac{1}{2})\sigma_{n+m-1}(0)\quad \quad (4.23)$

注意，这表达式并非关于 $n,m$ 对称：

$\int [\sigma_n,\sigma_m]=(m-n)\sigma_{n+m-1}$

我们看到了Virasoro代数。

关联函数一般包含三项不同的贡献：接触项，因子化项和体项。上面已经考察了接触项。因子化项来自曲面被夹断处。它们可写成关联函数因子化后，在各因子中插入 $\sigma_i$ ，再遍历插入方式求和，一般的形式是

$\left.\left\langle\sigma_{i_{1}} \ldots \sigma_{i_{n}}\right\rangle_{g}\right|_{夹断}=\sum_{i+j=n-2} B_{i j}\left\langle\sigma_{i} \sigma_{i_{1}} \ldots \sigma_{i_{r}}\right\rangle_{g_{1}}\left\langle\sigma_{j} \sigma_{i_{r+1}} \ldots \sigma_{i_{n}}\right\rangle_{g_{2}}\quad \quad (4.25)$

$B_{ij}$ 是一些系数。体项描述模空间内部的贡献。相当惊人的是，可以证明由于接触项不对称，这些贡献为零。因子化项也能根据一致性完全确定： $B_{ij}=1$ 。因此，我们最终得到了拓扑引力关联函数的如下递归关系：

$\begin{aligned} \left\langle\sigma_{n} \prod_{k \in S} \sigma_{k}\right\rangle_{g}=&\sum_{k \in S}\left(k+\frac{1}{2}\right)\left\langle\sigma_{n+k-1} \prod_{k^{\prime} \neq k} \sigma_{k^{\prime}}\right\rangle_{g}+\sum_{i+j=n-2}\left\langle\sigma_{i} \sigma_{j} \prod \sigma_{k}\right\rangle_{g-1} \\ &+\sum_{g_{1} ; S=X \cup Y \atop i+j=n-2}\left\langle\sigma_{i} \prod_{k \in X} \sigma_{k}\right\rangle_{g_{1}}\left\langle\sigma_{j} \prod_{k \in Y} \sigma_{k}\right\rangle_{g-g_{1}} \end{aligned}\quad \quad (4.26)$

第一项是接触项，第二项来自柄被夹断处，第三项来自平凡的同调闭链被夹断处。贡献总来自模空间的边界，因此鬼数减小。事实上，要么是亏格减小，要么是算符的数目减小，递归到最后，因子只剩下球面上的三点函数，非零的只有

$\left\langle\sigma_{0} \sigma_{0} \sigma_{0}\right\rangle_{0}=1\quad \quad (4.27)$

以及环面上的单点函数，在这里的归一化下计算结果是

$\left\langle\sigma_{1}\right\rangle_{1}=\frac{1}{16}\quad \quad (4.28)$

5. 矩阵模型和KdV层次结构

我们顺利地走到了连接拓扑场论和矩阵模型结果的路上，这也是拓扑引力和 $d<1$ 量子引力发生关联的地方。核心想法我们已经强调过多次：可在作用量中加入算符积分，对拓扑模型作微扰。这些算符的共形维数是 $(1,1)$ ，因而不破坏广义协变性。这样就能从拓扑场论开始，定义新的模型。我们将展示，选取特定的物质理论时，这些新的微扰的模型将对应矩阵模型的（多重）临界点。

5.1 多重临界点

为同矩阵模型建立关联，我们必须对拓扑模型作微扰。我们将首先考虑纯拓扑引力（ $d=0$ ），上节已经求解过它的关联函数了。这将容许我们同单矩阵模型的结果建立关联。为同时考察所有关联函数的微扰，先对所有亏格求和，并用弦耦合常数 $\lambda$ 的幂加权，以定义弦自由能

$F(t)=\sum_{g=0}^{\infty} \lambda^{2 g-2} F_{g}(t), \quad F_{g}(t)=\left\langle\exp \sum_{n} t_{n} \int \sigma_{n}\right\rangle_{g}\quad \quad (5.1)$

弦配分函数定义为 $Z=e^{F}$ ，它也包含不连通的弦图。这样对纯拓扑引力作微扰，会得到由不同耦合常数 $t_n$ 标记的，无穷维的理论空间，这可看成调整原来的作用量：

$S \rightarrow S-\sum t_{n} \int \sigma_{n}\quad \quad (5.2)$

方便起见，平移耦合常数： $t_1\to t_1+1$ ，这样拓扑引力背景就对应 $t_n=\delta_{n,1}$ 。

我们想找到这空间中的临界点，它们对应单矩阵模型的各多重临界点。这些点由整数 $k$ 标记，描述与 $(2,2k-1)$ 极小共形场论耦合的二维量子引力。

首先需要识别出胀子算符，考察它的角色。胀子算符 $D$ 衡量（带孔）曲面的总曲率积分。对亏格为 $g$ ，插入 $s$ 个算符的曲面，这是Euler示性数 $\chi=2g-2+s$ 。由 $(4.13)$ ， $\sigma_{n} \sim \hat{R}^{n}$ ， $\hat{R}$ 是世界面曲率，因此 $\sigma_1$ 可能是胀子算符。要更具体的话，考虑关联函数

$\left\langle\sigma_{1} \prod_{i=1}^{s} \sigma_{n_{i}}\right\rangle_{g}$

，应用递归关系 $(4.26)$ 。没有来自曲面被夹断处的贡献，因为不能满足相应的选择规则。只有接触项有贡献。我们得到

$\left\langle\sigma_{1} \prod_{i} \sigma_{n_{i}}\right\rangle_{g}=\sum_{i}\left(n_{i}+\frac{1}{2}\right)\left\langle\prod_{i} \sigma_{n_{i}}\right\rangle_{g}=\frac{3}{2}(2 g-2+s)\left\langle\prod_{i} \sigma_{n_{i}}\right\rangle_{g}\quad \quad (5.3)$

这里用了 $U(1)$ 守恒律 $(4.15)$ 。由此我们看到

$D=\frac{2}{3} \sigma_{1}\quad \quad (5.4)$

现在回忆一下， $\sigma_i$ 的关联函数是自由能的导数：

$\left\langle\sigma_{n_{1}} \ldots \sigma_{n_{s}}\right\rangle_{g}=\frac{\partial^{s} F_{g}}{\partial t_{n_{1}} \ldots \partial t_{n_{s}}}\quad \quad (5.5)$

加上 $U(1)$ 守恒律 $(4.15)$ 和胀子方程 $(5.3)$ ，得到函数 $F_g(t)$ 的两个标度律

$\sum_{n=0}^{\infty}(n-1) t_{n} \frac{\partial F_{g}}{\partial t_{n}}=(3 g-3) F_{g}\quad \quad (5.6)$

和（回忆一下，作了平移 $t_1\to t_1+1$ ）

$\sum_{n=0}^{\infty} t_{n} \frac{\partial F_{g}}{\partial t_{n}}=-(2 g-2) F_{g}\quad \quad (5.7)$

如果将耦合常数 $t_0$ 解释成宇宙学常数 $x$ ， $(5.6)$ 就给出拓扑引力关联函数的如下标度行为：

$\left\langle\sigma_{n_{1}} \ldots \sigma_{n_{s}}\right\rangle_{g} \sim x^{\sum\left(n_{i}-1\right)-3(g-1)}\quad \quad (5.8)$

那么 $\sigma_n$ 的共形维数是 $\Delta_n=n$ ， $\gamma_{st}=-1$ 。这里我们令宇宙学常数可自由取，其它的 $t_n$ 则看作理论的参数。

与此类似，我们也可沿 $t_k$ 轴展开，也就是耦合常数 $t_k$ 取非零的值。这对应单矩阵模型的多重临界点，可以这样看到：我们取两个标度律 $(5.6),(5.7)$ 的线性组合，以消去 $t_k$ 项。于是 $(5.6)$ 换成新的标度律

$\sum\left(\frac{n}{k}-1\right) t_{n} \frac{\partial F_{g}}{\partial t_{n}}=\left(2+\frac{1}{k}\right)(g-1) F_{g}\quad \quad (5.9)$

这给出标度行为

$\left\langle\sigma_{n_{1}} \ldots \sigma_{n_{s}}\right\rangle_{g} \sim x^{\sum \Delta_{n}-s-(2-\gamma)(g-1)}\quad \quad (5.10)$

其中 $\Delta_n=n/k$ ， $\gamma_{st}=-1/k$ 。注意，现在 $\sigma_k$ 的共形维数是1，扮演着胀子的角色。这些正是与量子引力耦合的 $(2,2k-1)$ CFT的KPZ结果^[26]。这应当看成微扰空间中的模型对应单矩阵模型的多重临界点的第一个信号。

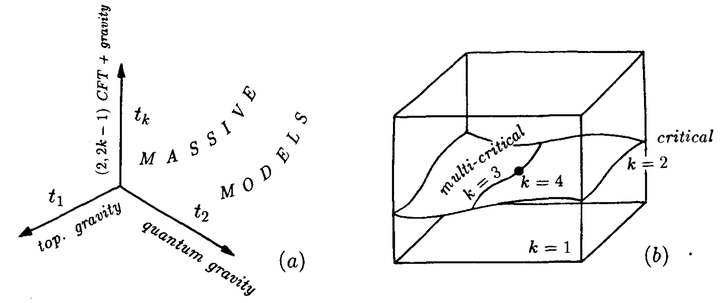
图10：对拓扑引力作微扰能得到的场论空间(a)，和对应的矩阵模型势形变的空间(b)。记号在文中有解释。

因此我们最终得到，从拓扑引力开始能到达的“理论空间”如图10。这是由坐标 $t_n$ 标记的无穷维向量空间。临界模型可在 $t$ 轴上找到。轴 $t_1 \neq 0$ 对应纯拓扑引力，其它轴 $t_k \neq 0$ 描述与量子引力耦合的 $(2,2k-1)$ 极小共形模型。特别地，轴 $t_2 \neq 0$ 代表纯二维量子引力。我们看到，它同拓扑引力的关联非常简单。 $t$ 空间中一般的点代表与引力耦合的有质量量子场论。原点 $t_n=0$ 是个奇点。这与矩阵模型势 $V(X)=\sum_{k} g_{k} \operatorname{Tr} X^{k}$ 的类似空间很不一样，临界点在这里对应余维数越来越高的特定子空间。

5.2 Virasoro代数

上面将胀子方程改写成自由能的线性微分方程。读者可能会想，对4.3节推出的算符 $\sigma_n$ 的递归关系，能作同样的操作吗？回忆一下这递归关系的一般形式：

$\begin{aligned} \left\langle\sigma_{n} \prod_{m \in S} \sigma_{m}\right\rangle_{g}=&\sum_{m \in S}\left(m+\frac{1}{2}\right)\left\langle\sigma_{n+m-1} \prod_{m^{\prime} \neq m} \sigma_{m^{\prime}}\right\rangle_{g}+\sum_{i+j=n-2}\left\langle\sigma_{i} \sigma_{j} \prod_{m \in S} \sigma_{m}\right\rangle_{g-1} \\& +\sum_{g_{1} ; S=X \cup Y \atop i+j=n-2}\left\langle\sigma_{i} \prod_{k \in X} \sigma_{k}\right\rangle_{g_{1}}\left\langle\sigma_{j} \prod_{k \in Y} \sigma_{k}\right\rangle_{g-g_{1}} \end{aligned}\quad \quad (5.11)$

虽然这关于自由能 $F_g$ 显然是非线性的，但由于精彩的关系 $Z^{-1} \partial^{2} Z=\partial^{2} F+(\partial F)^{2}$ ，用配分函数 $Z=e^F$ 写将是线性的：我们有

$\frac{\partial Z}{\partial t_{n}}=\sum\left(m+\frac{1}{2}\right) t_{m} \frac{\partial Z}{\partial t_{n+m-1}}+\left\{\begin{aligned} &\sum_{i+j=n-2} \frac{1}{2} \lambda^{2} \frac{\partial^{2} Z}{\partial t_{i} \partial t_{j}} &(n \geq 2) \\ &\frac{1}{16} Z &(n=1) \\ &\frac{1}{8} \lambda^{-2} t_{0}^{2} Z &(n=0) \end{aligned}\right.\quad \quad (5.12)$

第一项中的 $t_m$ 和 $\partial/\partial t_{n+m-1}$ 分别用于除去 $\sigma_m$ 和加入 $\sigma_{n+m-1}$ ，代表接触项的贡献。二阶导（ $n\geq 2$ ）描述因子化项。加入弦耦合常数 $\lambda$ 的幂是考虑到亏格， $n=1$ 时的 $1/16$ 来自 $\left\langle \sigma_1 \right\rangle_1$ ， $n=0$ 时的 $t_0^2$ 那项是 $\left\langle \sigma_0\sigma_0\sigma_0 \right\rangle_0=1$ 的结果。这些事实上是矩阵模型中的Schwinger-Dyson方程^[9]，应当看作拓扑弦论的运动方程。注意，这些总是联系起不同亏格的曲面，因而本质上是“弦的”。

$(5.12)$ 右边的微分算符记作 $L_{n-1}$ ：

$\frac{\partial Z}{\partial t_{n}}=L_{n-1} Z\quad \quad (5.13)$

$L_n$ 构成了Virasoro代数（的一部分）：

$\left[L_{n}, L_{m}\right]=(n-m) L_{n+m}\quad \quad (5.14)$

因为只考虑了正的 $L_n$ 模，不会出现中心荷。用容易想到的方式定义负模的话，将发现 $c=1$ 。事实上，Virasoro生成元可形式上写成手征标量场 $\Phi(z)$ 能动张量的模式，它满足 $\mathbb{Z}_2$ 扭条件 $\Phi(e^{2\pi i}z)=-\Phi (z)$ 。考虑 $\partial \Phi(z)$ 的模式展开

$\partial \Phi(z)=\sum \alpha_{n+\frac{1}{2}} z^{-n-\frac{3}{2}}\quad \quad (5.15)$

产生湮灭算符 $\alpha$ 可写成相干态表示

$\alpha_{n+\frac{1}{2}}=\lambda \frac{\partial}{\partial t_{n}}, \quad \alpha_{-n-\frac{1}{2}}=\lambda^{-1}\left(n+\frac{1}{2}\right) t_{n}, \quad(n \geq 0)\quad \quad (5.16)$

我们可以形式上定义能动张量为

$T(z)=: \frac{1}{2}[\partial \Phi(z)]^{2}:+\frac{1}{16 z^{2}}=\sum L_{n} z^{-n-2}\quad \quad (5.17)$

模式 $L_n$ 给出上述微分算符。

要找到多重临界点处的弦运动方程，我们在 $t_k=1$ ，而不是 $t_1=1$ 附近作微扰。这样Virasoro约束将变为

$\frac{\partial Z}{\partial t_{n+k-1}}=L_{n-1} Z\quad \quad (5.18)$

这方程告诉我们，除了 $\sigma_0,...,\sigma_{k-2}$ ，所有算符都可借助递归关系消去。这些场刚好对应极小 $(2,2k-1)$ CFT中的初级算符。其中场 $\sigma_n$ ， $n>k-2$ 可看作冗余的——它们可借助运动方程消去。

5.3 圈方程

接着简要讨论同圈方程的关联，更多细节见^[8]。再次考虑满足扭条件的标量

$\partial \Phi(z)=\sum \alpha_{n+\frac{1}{2}} z^{-n-\frac{3}{2}}\quad \quad (5.19)$

定义算符 $w(z)$ 为这展开的不高于负一次幂部分：

$w(z) \equiv(\partial \Phi)_{-}=\sum_{n=0}^{\infty} \alpha_{n+\frac{1}{2}} z^{-n-\frac{3}{2}}\quad \quad (5.20)$

这里产生算符 $\alpha_{n+\frac{1}{2}}$ 对应插入算符 $\sigma_n$ ，因此我们可等价地写

$w(z)=\sum_{n=0}^{\infty} \sigma_{n} z^{-n-\frac{3}{2}}\quad \quad (5.21)$

为这些算符引入源

$J(z)=\sum_{n=0}^{\infty} t_{n} z^{n+\frac{1}{2}}\quad \quad (5.22)$

于是

$(\partial \Phi)_{+}=\sum_{n=0}^{\infty}\left(n+\frac{1}{2}\right) t_{n} z^{n-\frac{1}{2}}=\frac{\partial J}{\partial z}\quad \quad (5.23)$

因此 $\partial \Phi(z)=w(z)+\partial J(z)$ 。那么，Schwinger-Dyson方程可重写成

$\left[J^{\prime}(z)\langle w(z)\rangle\right]_{<}+\frac{1}{2} \lambda^{2}\left\langle w^{2}(z)\right\rangle+\frac{1}{2}\langle w(z)\rangle^{2}+\frac{\lambda^{2}}{16 z^{2}}+\frac{t_{0}^{2}}{8 z}=0\quad \quad (5.24)$

这里 $<$ 指取 $z$ 的不高于负一次幂部分。算符 $w(z)$ 事实上是圈算符 $w(l)$ 的Laplace变换，它产生长为 $l$ 的圈：

$w(z)=\int_{0}^{\infty} d l e^{-l z} w(l)\quad \quad (5.25)$

这容许我们将 $(5.24)$ 重写成圈方程（见本次冬季学校中Brézin的讲义）。对 $k$ 重临界点这特别有趣：

$\begin{aligned} \frac{1}{2}\left(\frac{\partial}{\partial \ell}\right)^{k-\frac{1}{2}}\langle w(\ell)\rangle=& \frac{\lambda^{2} \ell}{16}+\frac{t_{0}^{2}}{8}+\int_{0}^{\infty} d \ell^{\prime} \ell^{\prime} J\left(\ell^{\prime}\right)\left\langle w\left(\ell+\ell^{\prime}\right)\right\rangle \\ & \frac{1}{2} \int_{0}^{\ell} d \ell^{\prime}\left(\lambda^{2}\left\langle w\left(\ell^{\prime}\right) w\left(\ell-\ell^{\prime}\right)\right\rangle+\left\langle w\left(\ell^{\prime}\right)\right\rangle\left\langle w\left(\ell-\ell^{\prime}\right)\right\rangle\right) \end{aligned}\quad \quad (5.26)$

这可像通常的圈方程一样解释^[27]：对边界的变分（左边），要么导致两圈相连，要么导致圈分裂成两部分（右边）。两常数项是亏格为0和1时额外对称性的结果。^[28]中从矩阵观点推出了类似的圈方程。

5.4 KdV层次结构

现在讨论，我们写成Virasoro约束的拓扑引力解，如何对应通常写成KdV方程的单矩阵模型解。Brézin和Migdal的讲义中有解释，矩阵模型中根本的方程是所谓的弦方程^[14]

$\sum t_{n}\left(n+\frac{1}{2}\right) R_{n}[u]+x=0, \quad u=F^{\prime \prime}=\left\langle\sigma_{0} \sigma_{0}\right\rangle\quad \quad (5.27)$

这里， $x=t_0$ 是宇宙学常数， $R_n$ 是Gelfand-Dikii多项式，递归地定义为

$R_{n+1}^{\prime}[u]=\left\{\frac{1}{2} \lambda^{2} \partial_{x}^{3}+2 u \partial_{x}+u^{\prime}\right\} R_{n}[u]\quad \quad (5.28)$

常数 $t_n$ 扮演着和上面相同的角色——它们是算符 $\sigma_n$ 的耦合常数。可进一步证明，函数 $u$ 事实上是KdV势。也就是说，它满足微分方程的层次结构

$\frac{\partial u}{\partial t_{n}}=\frac{\partial}{\partial x} R_{n+1}[u]\quad \quad (5.29)$

，是所谓的KdV流。（等价的说法是，配分函数 $Z=e^F$ 是KdV层次结构的 $\tau$ 函数。）由此我们可写

$\left\langle\sigma_{n} \sigma_{0} \sigma_{0}\right\rangle=\frac{\partial u}{\partial t_{n}}=\frac{\partial}{\partial x} R_{n+1}[u] \quad \Leftrightarrow\quad \left\langle\sigma_{n} \sigma_{0}\right\rangle=R_{n+1}[u]\quad \quad (5.30)$

于是弦方程可重写成（回忆一下， $x=t_0$ ）

$\sum\left(n+\frac{1}{2}\right) t_{n}\left\langle\sigma_{n-1} \sigma_0\right\rangle+t_{0}=0\quad \quad (5.31)$

再积分一次得到

$\left\{\sum\left(n+\frac{1}{2}\right) t_{n} \frac{\partial}{\partial t_{n-1}}+\frac{1}{2} t_{0}^{2}\right\} Z=L_{-1} Z=0\quad \quad (5.32)$

也就是说，我们推出了第一条Virasoro方程。那么，矩阵模型解可写成对配分函数 $Z(t)$ 的简单形式：

$\begin{aligned} &(i) \ \ L_{-1} Z=0\\ &(ii) \ Z 是\text{KdV}层次结构的\tau函数 \end{aligned}\quad \quad (5.33)$

可以证明，这事实上等价于

$L_{n} Z=0, \quad n \geq-1\quad \quad (5.34)$

这是因为，用Gelfand-Dikii多项式的递归关系，可从 $L_{n-1}Z=0$ 推出 $L_nZ=0$ ^[8]。现在，单矩阵模型与拓扑引力如何对应解释完了。

5.5 多矩阵模型

现在简要描述一下所有这些到多矩阵模型的推广，这对应带非平凡物质部分（ $d\neq 0$ ）的拓扑弦论。我们从矩阵模型开始，先简要介绍一下写成广义KdV层次结构的，一般矩阵链模型的Douglas解^[15]。我们不会解释如何从矩阵模型得到这个解，这点建议看其它人的讲义。

在Douglas的原始推导中，他考虑了 $q-1$ 个矩阵构成的链。他发现了根本的关系

$[P,Q]=1\quad \quad (5.35)$

其中 $P,Q$ 是微分算符

$\begin{aligned} &Q=D^{q}-\frac{1}{q} \sum_{i=0}^{q-2} u_{i}(x) D^{i}\\ &P=D^{p}-\frac{1}{p} \sum_{i=0}^{p-2} v_{i}(x) D^{i} \end{aligned}\quad \quad (5.36)$

这可用矩阵积分直接定义，但这里不必了解。 $D=\lambda \partial/\partial x$ ， $x$ 是宇宙学常数， $\lambda$ 是弦耦合常数。 $u_i(x),v_i(x)$ 是待确定的函数。这些函数的含义从矩阵模型角度不能立刻看出，除了 $u_{q-2}$ ，它对应孔-孔两点函数

$u_{q-2}=F^{\prime \prime}=\left\langle\sigma_{0} \sigma_{0}\right\rangle\quad \quad (5.37)$

算符 $P$ 由 $Q$ 按如下方式定义：首先将 $Q$ 的 $q$ 次方根形式上定义成Laurent级数

$L=Q^{1/q}=D+\sum_{i=1}^\infty f_i D^{-i}\quad \quad (5.38)$

$L$ 是伪微分算符，这是微分算符的推广，容许导数 $D$ 的负次幂。这些负次幂满足对易关系

$D^{-1} g=g D^{-1}+\sum_{i=1}^{\infty}(-1)^{i} g^{(i)} D^{-i-1}\quad \quad (5.39)$

那么

$g=D^{-1} D g=D^{-1}\left(g^{\prime}+g D\right)\quad \quad (5.40)$

一般的伪微分算符形如

$K=\sum_{i=-\infty}^{N} k_{i} D^{i} \equiv K_{+}+K_{-}\quad \quad (5.41)$

其中 $K_{+}=\sum_{i=0}^{N} k_{i} D^{i}$ 是微分算符部分。我们也定义 $K$ 的留数为 $\operatorname{res}(K)=k_{-1}$ 。用这些概念， $P$ 由 $Q$ 定义为

$P=\left(L^{p}\right)_{+}= (Q^{p / q} )_{+}\quad \quad (5.42)$

弦方程换成了关系 $[P,Q]=1$ ，它将用于确定未知函数 $u_i(x)$ 。为了解它们的含义，我们考虑广义KdV流，它由Lax方程

$\frac{\partial Q}{\partial t_{n-1}}=\left[L_{+}^{n}, Q\right]=\left[Q, L_{-}^{n}\right]\quad \quad (5.43)$

定义，第二个等号用了 $0=\left[L^{n}, Q\right]=\left[L_{+}^{n}+L_{-}^{n}, Q\right]$ 。我们将流 $\partial/\partial t_n$ 记作算符 $\mathcal{O}_n$ ， $\mathcal{O}_{0}=\mathcal{P}$ 是孔算符，之前记作 $\sigma_0$ 。回忆一下 $u_{q-2}=\langle \mathcal{P}\mathcal{P}\rangle$ ，KdV流的条件是

$\left\langle\mathcal{P} \mathcal{P} \mathcal{O}_{n-1}\right\rangle=\frac{\partial u_{q-2}}{\partial t_{n-1}}\quad \quad (5.44)$

为计算右边，我们要从 $\left[Q, L_{-}^{n}\right]$ 中提出 $D^{q-2}$ 项，结果是

$\left\langle\mathcal{P} \mathcal{P} \mathcal{O}_{n-1}\right\rangle=\frac{\partial u_{q-2}}{\partial t_{n-1}}=\frac{\partial}{\partial x} \operatorname{res}\left(L^{n}\right)\quad \quad (5.45)$

积分给出

$\left\langle\mathcal{P} \mathcal{O}_{n-1}\right\rangle=\operatorname{res}\left(L^{n}\right)\quad \quad (5.46)$

留数 $\operatorname{res}\left(L^{n}\right)$ 是函数 $u_i(x)$ 及其导数的多项式。特别地，对前 $q-1$ 个流 $\mathcal{O}_i$ （ $i=0,...,q-2$ ），我们有

$\langle \mathcal{P}\mathcal{O}_i\rangle \sim u_{q-2-i}+修正\quad \quad (5.47)$

例如

$\langle \mathcal{P}\mathcal{O}_1\rangle \sim u_{q-3}+u_{q-2}'\quad \quad (5.48)$

总结一下，在多矩阵模型中，算符 $\mathcal{O}_{n-1}$ 是 $L^n$ 生成的流。如果 $n=k\cdot q$ ，那么显然没有相应的流，因为 $L^{kq}=Q^k$ 与 $Q$ 对易。所以，谱有点像是能带。第一条能带包含前 $q-1$ 个算符 $\mathcal{O}_{0}, \ldots, \mathcal{O}_{q-2}$ ，接着在应当出现 $\mathcal{O}_{q-1}$ 处存在能隙。

这种能带结构可同拓扑弦论对应起来^[6]。我们的物质部分中有 $q-1$ 个初级场 $\phi_i=\mathcal{O}_i$ ，这是第一条能带上的算符。第二条能带包含第一次级场 $\sigma_1(\phi_i)$ ，依此类推： $\sigma_{n}\left(\phi_{i}\right)=\mathcal{O}_{n q+i}$ 。因此显然需要带 $q-1$ 个物理态 $\phi_i$ 的拓扑物质系统，也不难知道荷 $q_i$ 和 $d$ 是

$q_{i}=\frac{i}{q}, \quad d=\frac{q-2}{q}\quad \quad (5.49)$

5.6 扭 $\mathcal{N}=2$ 极小模型

寻找对应拓扑模型的问题，由Li^[11]优雅地解决了，他跟进Eguchi和Yang^[10]，考虑扭 $\mathcal{N}=2$ 极小模型。这些模型确实有 $d=c/3=k/(k+2)$ ， $k=0,1,...$ 。对给定的 $k$ ，可能不止一个模型。它们由ADE类型的Lie群 $G$ 标记，这可能同它们是像Dynkin图一样的链上的格点模型有关。群 $G$ 需要满足Coxeter数 $h_G=k+2$ 。幸运的是，这些 $\mathcal{N}=2$ 模型有一类代表是Landau-Ginzburg理论^[23]^[24]。

3.3节说过，Landau-Ginzburg模型有极好的性质：手征初级场的关联函数由超势完全确定。这些场扭后刚好对应物理算符。事实上，对准齐次的势 $W(X_a)$ ，算符代数就是多项式环

$\mathcal{H}_{物理}=\frac{\mathbb{C}\left[X_{a}\right]}{\partial W\left(X_{a}\right)}\quad \quad (5.50)$

$\mathbb{C}\left[X_{a}\right]$ 是 $X_a$ 多项式的集合。对应极小模型的超势是

$\begin{array}{ll} A_{n}: & W=X^{n+1} \\ D_{n}: & W=X^{n-1}+X Y^{2}\\ E_{6}: & W=X^{3}+Y^{4} \\ E_{7}: & W=X^{3}+X Y^{3} \\ E_{8}: & W=X^{3}+Y^{5} \end{array}\quad \quad (5.51)$

一般地，我们考虑这些超势保持准齐次性的变体，例如 $W=X^{3}+Y^{3}+Z^{3}+a X Y Z$ ，这引入一个模空间坐标 $a$ 。但ADE势的模空间是零维的，理论也就没有边缘的形变。事实上，只有这些势有这性质，这也是ADE分类出现在奇点理论中的原因。不难知道这些环是什么。例如， $A_n$ 环是 $X$ 的多项式模去 $X^n=0$ ，那么它的基是

$\left\{1, X, X^{2}, \ldots, X^{n-1}\right\}\quad \quad (5.52)$

类似地， $E_6$ 环是 $X,Y$ 的多项式模去 $\partial_{X} W=X^{2}=0$ 和 $\partial_{Y} W=Y^{3}=0$ ，那么基是

$\left\{1, X, Y, X Y, Y^{2}, X Y^{2}\right\}\quad \quad (5.53)$

基本场的 $U(1)$ 荷，通过变换 $X_a\to \lambda^{q_a}X_a$ 下势的标度行为确定。于是场 $\phi_i$ 的荷是 $q_i=i/(k+2)$ ， $i,0\leq i\leq k$ 是一个整数。更具体地说，对simply-laced Lie群 $G$ 标记的模型， $i+1$ 是 $G$ 的指数， $k+2$ 是 $G$ 的Coxeter数，这些数据列在表2中。

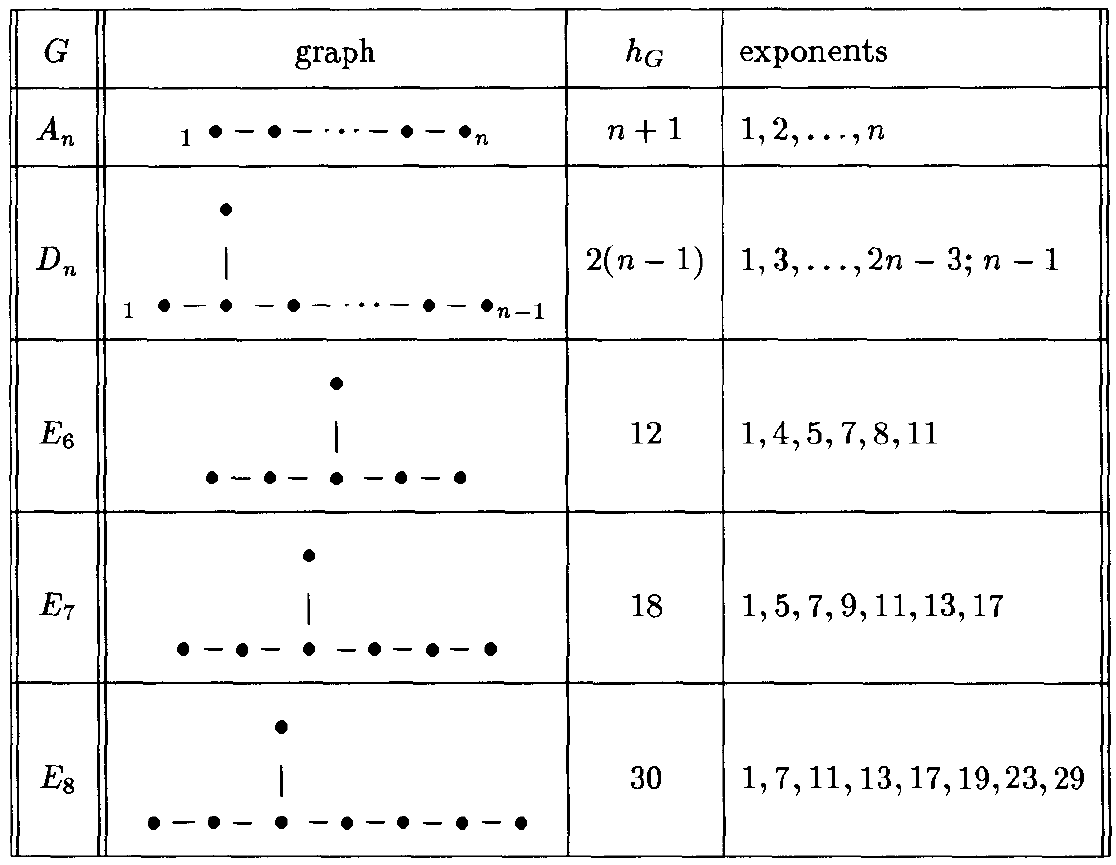
表2：simply-laced Lie群的Dynkin图，Coxeter数$h_G$和指数。

Landau-Ginzburg环结构大幅简化了拓扑场论中的计算。回忆一下，我们想计算如下形式的关联函数：

$\left\langle\phi_{i_{1}} \ldots \phi_{i_{s}} \int \phi_{j_{1}} \ldots \int \phi_{j_{r}}\right\rangle_{g}\quad \quad (5.54)$

这可因子化成

$\left\langle\phi_{i_{1}} \phi_{i_2}\phi_{i_3} \int \phi_{j_{1}} \ldots \int \phi_{j_{r}}\right\rangle_{0}\quad \quad (5.55)$

2.7节说过，这些关联函数由微扰三点函数

$c_{i j k}(t)=\left\langle\phi_{i} \phi_{j} \phi_{k} \exp \left(\sum_{n} t_{n} \int \phi_{n}\right)\right\rangle_{0}\quad \quad (5.56)$

生成，因此我们需要计算的就是这个。具体起见，我们只考虑 $A_{k+1}$ 模型， $\phi_i\equiv X^i$ ， $i=0,1,...,k$ 。环 $(5.52)$ 给出的算符乘积展开是

$\phi_{i} \cdot \phi_{j}=\left\{\begin{aligned} &\phi_{i+j}, \ i+j \leq k \\ &0, \ \ \ \ \ \text {其它情形} \end{aligned}\right.\quad \quad (5.57)$

微扰理论的超势形如

$W=\frac{X^{k+2}}{k+2}-\sum_{i=0}^{k} g_{i}(t) X^{i}\quad \quad (5.58)$

右边额外的项不是简单的 $t_iX^i$ 形式，因为我们只知道在共形（ $t=0$ ）处 $\phi_i=X^i$ ，所以 $g_{i}=t_{i}+\mathcal{O}\left(t^{2}\right)$ 。场 $\phi_i$ 定义为

$\phi_{i}(X)=-\frac{\partial W(X)}{\partial t_{i}}=\sum_{j=0}^{k} \frac{\partial g_{j}}{\partial t_{i}} X^{j}\quad \quad (5.59)$

我们想计算函数 $g_i(t)$ ，这等价于计算场 $\phi_i(X)$ 。

我们已经在3.2节看到，拓扑共形场论中度规 $\left\langle\phi_{i} \phi_{j}\right\rangle=\eta_{i j}=c_{i j 0}$ 为常数。那么，在微扰TCFT的空间中我们就总有平坦度规，可选取坐标 $t_i$ 以使这度规为常数。我们将用这点来确定关联函数。注意，对给定的超势 $W$ ，算符乘积是完全确定的，由多项式环给出：

$\phi_{i}(X) \phi_{j}(X)=\sum c_{i j}{ }^{l} \phi_{l}(X) \quad (\text{mod} \ W^{\prime}(X))\quad \quad (5.60)$

现在两边取期望值。 $t=0$ 时，由荷守恒，只有场 $\phi_k$ 的期望值非零。 $t\neq 0$ 时仍是如此，因为 $\int \phi_l^{(2)}$ 的凝聚态带荷 $q_l=l/(k+2)-1 <1$ 。所以内积应当满足

$\left\langle\phi_{i} \phi_{j}\right\rangle=c_{i j}{}^{k}(t)\quad \quad (5.61)$

这给出唯一的式子

$\left\langle\phi_{i} \phi_{j}\right\rangle=\oint \frac{d x}{2 \pi i} \frac{\phi_{i}(X) \phi_{j}(X)}{W^{\prime}(X)}\quad \quad (5.62)$

显然这保持算符代数 $(5.60)$ ，因为正比于 $W'(X)$ 的项没有贡献。我们知道，场 $\phi_i$ 间应当关于这内积正交。这些正交多项式可通过如下的优雅方式，定义成超势分数次幂的导数：

$\phi_{i}(X)=\frac{\partial}{\partial x} \frac{ (L^{i+1} )_{+}}{i+1}, \quad W=\frac{L^{k+2}}{k+2}\quad \quad (5.63)$

和之前一样，这里 $+$ 指取 $X$ 的正次幂部分。容易验证

$\begin{aligned} \left\langle\phi_{i} \phi_{j}\right\rangle &=\oint \frac{d x}{2 \pi i} \frac{ (L^{i} \partial_{x} L )_{+} (L^{j} \partial_{x} L )_{+}}{L^{k+1} \partial_{x} L}&(5.64) \\ &=\oint \frac{d x}{2 \pi i} L^{i+j-k-1} \frac{\partial L}{\partial x}=\delta_{i+j, k} &(5.65) \end{aligned}$

现在我们有了物理场 $\phi_i$ 的两种定义： $(5.59)$ 和 $(5.63)$ 。它们应当一致，于是我们得到

$\frac{\partial W}{\partial t_{i}}=c \cdot \frac{\partial}{\partial x} (W^{\frac{i+1}{k+2}} )_{+}\quad \quad (5.66)$

$c$ 是某个常数。这个方程足够解出算符 $\phi_i$ 和耦合常数 $g_i(t)$ 了，结果是

$\phi_{i}(X)=(-1)^{i} \operatorname{det}\left(\begin{array}{ccccc} -X & 1 & 0 & \cdots & 0 \\ t_{k} & -X & 1 & \ddots & \vdots \\ t_{k-1} & t_{k} & \ddots & & 0 \\ \vdots & & \ddots & & 1 \\ t_{k-i+2} & \cdots & t_{k-1} & t_{k} & -X \end{array}\right)\quad \quad (5.67)$

我们完成了极小模型关联函数的计算。现在需要展示，这些计算与多矩阵模型的解一致。这里不说细节（见^[12]）了，大概说一下思路。首先观察到超势

$W=\frac{X^{k+2}}{k+2}-\sum g_{i}(t) X^{i}\quad \quad (5.68)$

和KdV算符

$Q=\frac{D^{k+2}}{k+2}-\sum u_{i}(x) D^{i}\quad \quad (5.69)$

很像，那么就知道 $(5.68)$ 事实上等价于KdV流方程

$\frac{\partial Q}{\partial t_{i}}= [(Q^{\frac{i+1}{k+2}} )_{+}, Q ]\quad \quad (5.70)$

现在，多矩阵模型与扭极小模型如何对应解释完了。

5.7 $W$ -约束

我们还只讨论了对应前 $q-1$ 个KdV流的初级场 $\phi_i$ 。引力次级场 $\sigma_n(\phi_i)$ 的计算更复杂^[11]，目前的了解还不像 $d=0$ 时那么清楚。不过解不难描述。配分函数 $Z(t)$ 仍是通过一系列Schwinger-Dyson方程确定，这是具有如下形式的线性微分方程：^[8]^[9]^[29]

$W_n^{(s)}Z=0,\quad n\geq 1-s\quad \quad (5.71)$

微分算符 $W_n^{(s)}$ 构成了所谓的 $W$ -代数，与标记极小模型的Lie群 $G$ 有关。它们是自旋 $s$ 的流，这是Virasoro代数的推广。对群 $G$ 中每个Casimir，我们有一个 $W$ -生成元。对这些关系的详细讨论超出了这份讲义的范围。

参考

^E. Witten, Commun. Math. Phys. 121 (1989) 351.
^J. Labastida, M. Pernici, and E. Witten, Nucl. Phys. B310 (1988) 611. D. Montano and J. Sonnenschein, Nucl. Phys. B313 (1989) 258 ; Nucl. Phys. 324 (1990) 348. R. Myers and V. Periwal, Nucl. Phys. 333 (1990) 536.
^E. Brézin and V. Kazakov, Phys. Lett. B236 (1990) 144. M. Douglas and S. Shenker, Nucl. Phys. B335 (1990) 635 . D.J. Gross and A. Migdal, Phys. Rev. Lett. 64 (1990) 127.
^^a^b^c^dE. Witten, Nucl. Phys. B340 (1990) 281.
^J. Distler, Nucl. Phys. B342 (1990) 523.
^^a^bR. Dijkgraaf and E. Witten, Nucl. Phys. B342 (1990) 486.
^^a^b^c^d^eE. Verlinde and H. Verlinde, Nucl. Phys. B348 (1991) 457.
^^a^b^c^dR. Dijkgraaf, E. Verlinde, and H. Verlinde, Nucl. Phys. B348 (1991) 435.
^^a^b^cM. Fukuma, H. Kawai, and R. Nakayama, Int. J. Mod. Phys. A6 (1991) 1385.
^^a^bT. Eguchi and S.-K. Yang, Mod. Phys. Lett A5 (1990) 176.
^^a^b^cK. Li, Caltech preprints CALT-68-1661, CALT-68-1670 (1990).
^^a^b^cR. Dijkgraaf, E. Verlinde, and H. Verlinde, Nucl. Phys. B352 (1991) 59.
^C. Vafa, Mod. Phys. Lett. A6 (1990) 337.
^^a^bD.J. Gross and A. Migdal, Nucl. Phys. B340 (1990) 333. T. Banks, M. Douglas, N. Seiberg, and S. Shenker, Phys. Lett. 238B (1990) 279.
^^a^bM. Douglas, Phys. Lett. 238B (1990) 176. P. Di Francesco and D. Kutasov, Nucl. Phys. B342 (1990) 589.
^^a^bR. Dijkgraaf, E. Verlinde, and H. Verlinde, ‘Notes on Topological String Theory and 2D Quantum Gravity,’ in String Theory and Quantum Gravity, Proceedings of the Trieste Spring School 1990, Eds. M. Green et al. (World-Scientific, 1991).
^^a^bE. Witten, Commun. Math. Phys. 117 (1988) 353.
^E. Witten, Commun. Math. Phys. 118 (1988) 411.
^P. van Baal, Acta Phys. Polon. B21 (1990) 73.
^D. Birmingham, M. Blau, M. Rakowski, and G. Thompson, ‘Topological Field theory,’ preprint CERN-TH 6045/91, to be published in Physics Reports.
^S. Shenker, ‘The Strength of Nonperturbative Effects in String Theory,’ in the proceedings of the Workshop on Random Surfaces, Quantum Gravity and Strings, Cargèse 1990 (Plenum Press, 1991).
^W. Lerche, C. Vafa, and N.P. Warner, Nucl. Phys B324 (1989) 427.
^^a^bE. Martinec, Phys. Lett. 217B (1989) 431; ‘Criticality, Catastrophe and Compactifications,’ V.G. Knizhnik memorial volume, 1989.
^^a^bC. Vafa and N. Warner, Phys. Lett. 218B (1989) 51.
^J. Distler and P. Nelson, Commun. Math. Phys. 138 (1991) 273.
^V. Knizhnik, A. Polyakov, A. Zamolodchikov, Mod. Phys. Lett. A3 (1988) 819. F. David, Mod. Phys. Lett. A3(198) 1651. J. Distler and H. Kawai, Nucl. Phys. B321 (1989) 509.
^A.A. Migdal, Phys. Rep. 102 (1983) 199.
^F. David, Mod. Phys. Lett A5 (1990) 1019.
^J. Goeree, ‘W Constraints in 2-D Quantum Gravity,’ Utrecht preprint THU-19 (1990). M. Fukuma, H. Kawai, and R. Nakayama, ‘Infinite Grassmannian Structure of Two-Dimensional Quantum Gravity,’ Tokyo preprint UT-572 (1990).

发布于 05-18

Download as PDF

理论物理：拓扑场论和二维量子引力【转载】

1. 引言

2. 拓扑场论

3. 拓扑共形场论

4. 拓扑弦论

5. 矩阵模型和KdV层次结构

参考

相关文章：

发表回复取消回复

理论物理：拓扑场论和二维量子引力【转载】

1. 引言

2. 拓扑场论

3. 拓扑共形场论

4. 拓扑弦论

5. 矩阵模型和KdV层次结构

参考

相关文章：

发表回复 取消回复

发表回复取消回复