本站相关文章:编程:MATLAB实现粒子二维随机运动轨迹
维基百科介绍:http://en.wikipedia.org/wiki/Random_walk
ArXiv中搜索关键字“Quantum Random Walk”后的结果:http://arxiv.org/find/all/1/all:+AND+Walks+AND+Random+Quantum/0/1/0/all/0/1
模拟器
引用自:http://demonstrations.wolfram.com/SimulatingTheSimpleRandomWalk/
简单介绍
A random walk is a mathematical formalization of a path that consists of a succession of random steps. For example, the path traced by amolecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the financial status of a gambler can all be modeled as random walks, although they may not be truly random in reality. The term random walk was first introduced by Karl Pearson in 1905.[1] Random walks have been used in many fields: ecology, economics, psychology, computer science, physics, chemistry, and biology.[2][3][4][5][6][7][8][9] Random walks explain the observed behaviors of processes in these fields, and thus serve as a fundamentalmodel for the recorded stochastic activity.
Various different types of random walks are of interest. Often, random walks are assumed to be Markov chains or Markov processes, but other, more complicated walks are also of interest. Some random walks are on graphs, others on the line, in the plane, or in higher dimensions, while some random walks are on groups. Random walks also vary with regard to the time parameter. Often, the walk is in discrete time, and indexed by the natural numbers, as in  . However, some walks take their steps at random times, and in that case the position
. However, some walks take their steps at random times, and in that case the position 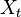 is defined for the continuum of times
is defined for the continuum of times 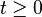 . Specific cases or limits of random walks include the Lévy flight. Random walks are related to the diffusion models and are a fundamental topic in discussions of Markov processes. Several properties of random walks, including dispersal distributions, first-passage times and encounter rates, have been extensively studied.
. Specific cases or limits of random walks include the Lévy flight. Random walks are related to the diffusion models and are a fundamental topic in discussions of Markov processes. Several properties of random walks, including dispersal distributions, first-passage times and encounter rates, have been extensively studied.

