Skip to content
TAHOLAB
TAHOLAB

华月凌衍·格物致知·温故知新

Primary Navigation Menu
Menu
  • 首页
  • 导航
    • 友情链接
    • 在线小工具
      • 显示带三位数毫秒的时间
      • 360全景图查看器
      • 实时卫星云图
      • Latex 转 Word 工具
      • 妈咪说的Latex在线公式编辑器
    • 我的
      • 华月凌衍斋
        • 我的语录
        • 我说
        • 我学到的知识
        • 我的收藏
        • 我读的书
        • 人物墙
        • 实验室
        • iLearn
        • 摘抄的文字
        • 记录一点科学
        • 评分的电影
      • 我的百度脑图
      • 我的可道云文件
      • 我的私人同步盘
    • 科研页
      • 已经发表的SCI学术论文
    • 睦乐黛黛紫
    • 大学物理虚拟仿真实验平台
    • 听一下音乐吧
    • 好的播客列表
  • 随机一篇
  • 目录
  • RSS
Secondary Navigation Menu
Menu
  • 科学
    • 物理学
    • 数学
    • 科普
    • 生物学
  • 技术
    • 电脑技术
    • 极客地带
    • 创客
    • 我的创客项目
    • 硬件Hardware
    • 编程
    • 人工智能
    • 黑客
  • 艺术
    • 纪录片科学，人文，大自然…… 在这里学习，在这里纪录。
    • 动画
    • MV
    • 绘画
    • 摄影
    • 音乐
  • 进步青年
    • 日语
    • 英语
    • 运动与旅行
    • 乐器
  • 我的生活
    • 生活记录
    • 我的评测
    • 评论与感悟
    • 随笔

物理学 (Page 5)

仿真+计算物理：官方 COMSOL 视频课程中心

2021-07-08
By: taho
On: 2021年7月8日
In: 仿真, 计算物理
With: 0 Comments

视频来自B站：COMSOL 2020全套视频教程 入门+模块（含讲义）_哔哩哔哩_bilibili 阅读全文

创客+计算物理：COMSOL教程——Halbach 转子的静磁场建模

2021-07-07
By: taho
On: 2021年7月7日
In: 创客, 计算物理
With: 0 Comments

全文来自：Halbach 转子的静磁场建模 (comsol.com) 本案例展示了外向磁通聚焦磁转子阅读全文

创客+计算物理：COMSOL教程——AC/DC 模块简介

2021-07-07
By: taho
On: 2021年7月7日
In: 创客, 计算物理
With: 0 Comments

内容来自COMSOL官网：COMSOL教程 – 电子, 电气 AC/DC 模块简介 AC阅读全文

创客+计算物理：用COMSOL模拟永磁体磁性的教程

2021-07-07
By: taho
On: 2021年7月7日
In: 创客, 计算物理
With: 0 Comments

全文来自：永磁体 (comsol.com) （COMSOL官网教程） 本案例是静磁问题的一个教程模型阅读全文

理论物理：拓扑场论和二维量子引力【转载】

2021-07-07
By: taho
On: 2021年7月7日
In: 理论物理, 量子引力
With: 0 Comments

全文转载自知乎：拓扑场论和二维量子引力 – 知乎 (zhihu.com) 1. 引言 过阅读全文

电脑技术：COMSOL 教程合集

2021-06-18
By: taho
On: 2021年6月18日
In: 建模, 物理学, 电脑技术, 计算物理
With: 0 Comments

以下内容均来自COMSOL 官网。 电子书 下载 PDF 版本 COMSOL 产品手册，或点击下方链阅读全文

TED演讲视频：The death of the universe — and what it means for life

2021-05-25
By: taho
On: 2021年5月25日
In: 报告和讲座, 物理学, 理论物理
With: 0 Comments

Katie Mack: The death of the universe — and 阅读全文

物理学：格点规范理论（lattice gauge theory）概念

2021-05-18
By: taho
On: 2021年5月18日
In: 物理学
With: 0 Comments

不知道这个格点规范场论是否可以描述格点时空？有待了解。 格点规范理论（lattice gauge t阅读全文

物理学：图形化演示视频 Waves: Light, Sound, and the nature of Reality

2021-05-02
By: taho
On: 2021年5月2日
In: 物理学, 理论物理
With: 0 Comments

Waves: Light, Sound, and the nature of Reality &#8阅读全文

电脑技术：一款游戏开发软件——Roblox（罗布乐思）

2021-03-31
By: taho
On: 2021年3月31日
In: 建模, 教育, 游戏制作
With: 0 Comments

这款软件现在可以用于游戏开发，也可以用于建模，也可以用于教学。 可以用于物理碰撞，模拟，特别适用于教阅读全文

讲座+数学+物理学：几个丘成桐演讲

2021-03-20
By: taho
On: 2021年3月20日
In: 报告和讲座, 数学, 物理学
With: 0 Comments

《开讲啦》 20160917 丘成桐：你为什么学不好数学？ YouTube：专访世界顶尖数学家 哈佛阅读全文

电脑技术：来自B站的 Manim 教程合集

2021-03-16
By: taho
On: 2021年3月16日
In: Python, 人机交互, 创客, 动画, 数学, 物理学, 电脑技术, 编程, 计算物理
With: 0 Comments

Manim教程合集 B站的这些视频来自YouTube，https://www.youtube.com阅读全文

物理学：麦克斯韦方程和规范理论的观念起源

2021-03-12
By: taho
On: 2021年3月12日
In: 理论物理
With: 0 Comments

杨振宁写的一篇科普性综述：麦克斯韦方程和规范理论的观念起源(The conceptual origi阅读全文

备查：2021年国家自然科学基金申请代码大全——数理学部

2021-02-27
By: taho
On: 2021年2月27日
In: 备查条目, 物理学, 理论物理
With: 0 Comments

2021年国科金申请正在进行时，数理学部的各类研究方向代码列表如下图，建议下载或在新窗口查看图片。阅读全文

物理学：《高等量子力学》（孙昌璞讲授）在线课程

2021-01-23
By: taho
On: 2021年1月23日
In: 报告和讲座, 教程, 物理学, 理论物理
With: 0 Comments

课程来源 这是由蔻享发布的《高等量子力学》课程，共34个视频。 课程链接： 孙昌璞（中国科学院院士、阅读全文

物理学：知乎上找到的一个系列文章——《Halbach array 的构建与模拟》

2021-01-22
By: taho
On: 2021年1月22日
In: DIY, 创客, 物理学, 科技发明, 飞行
With: 0 Comments

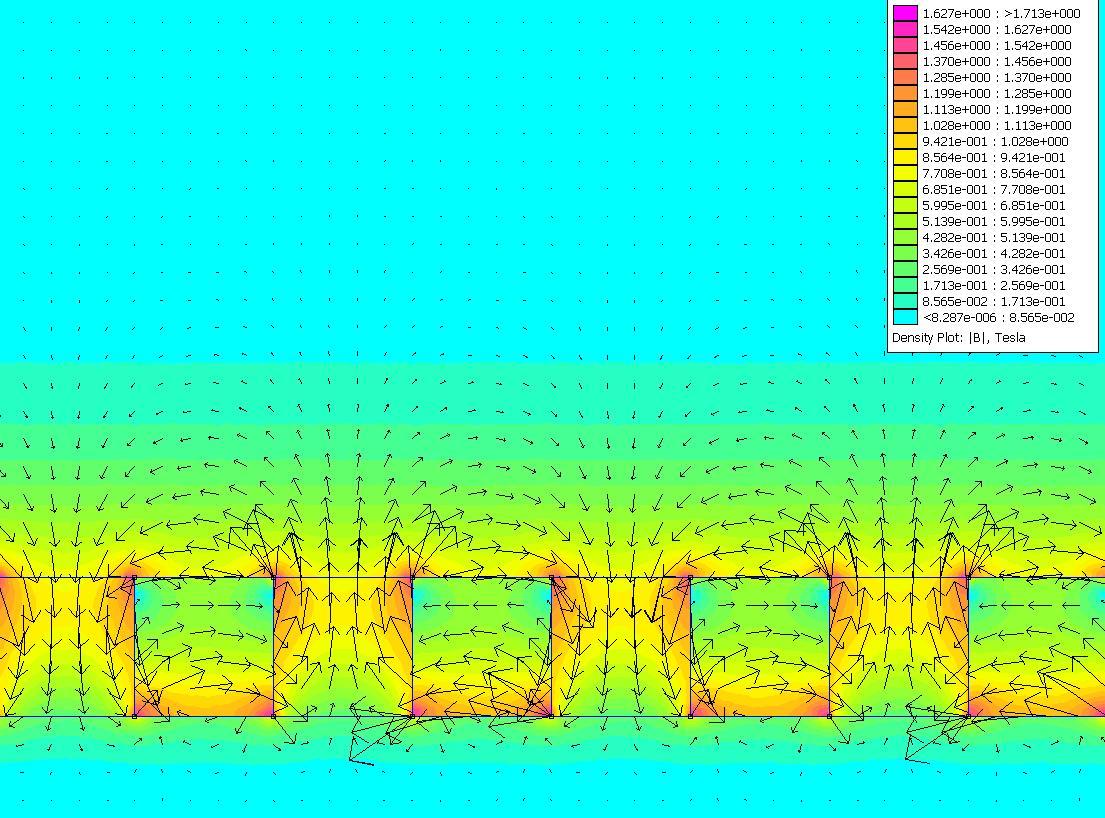
知乎上找到了一个系列文章——《Halbach array 的构建与模拟》，一共写了三篇，链接分别如下阅读全文

File:Linear Halbach Array (Weak side up).png

物理学：Halbach array（海尔贝克阵列/哈尔贝克/哈尔巴赫阵列）

2021-01-22
By: taho
On: 2021年1月22日
In: 创客, 物理学, 理论物理, 飞行
With: 0 Comments

  百度百科：Halbach Array一般指海尔贝克阵列，见 海尔贝克阵列_百度百科 (阅读全文

物理学+创客：一种增强单侧磁场的排列方式

2021-01-20
By: taho
On: 2021年1月20日
In: DIY, 创客, 物理学, 飞行
With: 0 Comments

HALBACH ARRAY How to double the power of magnets, 阅读全文

飞行：电磁悬浮四轴飞行（器）

2021-01-19
By: taho
On: 2021年1月19日
In: DIY, 创客, 极客地带, 科技发明, 飞行
With: 0 Comments

Electromagnetic Levitation Quadcopter – YouT阅读全文

物理学：引力波

2021-01-15
By: taho
On: 2021年1月15日
In: 理论物理, 量子引力
With: 0 Comments

描述引力波的理论与描述电动力学的电磁波的理论是类似的。 以下内容摘录自维基百科：引力波 &#8211阅读全文

物理学：暗能量候选者

2021-01-12
By: taho
On: 2021年1月12日
In: 物理学, 理论物理
With: 0 Comments

主要的暗能量的候选者如下： 宇宙学常数，Λ Quintessence，物态方程的阅读全文

物理学+数学：旋量简介

2021-01-02
By: taho
On: 2021年1月2日
In: 数学, 物理学
With: 0 Comments

知乎的回答： Clifford代数 和Clifford代数联系紧密的是四元数  ，它是  上的4维线阅读全文

物理学：神奇的量子纠缠（科学声音）

2020-12-31
By: taho
On: 2020年12月31日
In: 理论物理, 科教片
With: 0 Comments

内容硬核 ：什么是神奇的量子纠缠，必须得先从“EPR 实验”讲起。|《宇宙自然生命简史》第二十三集 阅读全文

物理学：An Epic Journey to a Black Hole to Give You Goosebumps

2020-12-31
By: taho
On: 2020年12月31日
In: 物理学, 理论物理, 量子引力
With: 0 Comments

(238) An Epic Journey to a Black Hole to Give You 阅读全文

文章分页

上一页 1 … 4 5 6 … 15 下一页

本站自2008年至2025年内容若未加说明，默认版权归TAHO所有，如有侵权请联系 tahoroom@163.com