数学：K函数

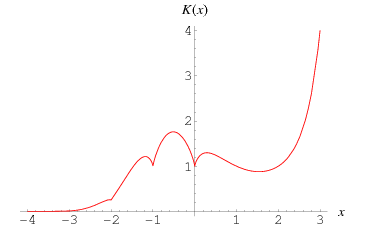
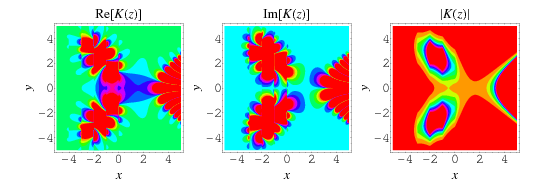
In mathematics, the K-function, typically denoted K(z), is a generalization of the hyperfactorial to complex numbers, similar to the generalization of the factorial to the gamma function.

Formally, the K-function is defined as

K(z)=(2\pi )^{(-z+1)/2}\exp \left[{\begin{pmatrix}z\\2\end{pmatrix}}+\int _{0}^{z-1}\ln(\Gamma (t+1))\,dt\right].

It can also be given in closed form as

K(z)=\exp \left[\zeta ^{\prime }(-1,z)-\zeta ^{\prime }(-1)\right]

where ζ'(z) denotes the derivative of the Riemann zeta function, ζ(a,z) denotes the Hurwitz zeta function and

\zeta ^{\prime }(a,z)\ {\stackrel {\mathrm {def} }{=}}\ \left[{\frac {\partial \zeta (s,z)}{\partial s}}\right]_{s=a}.

Another expression using polygamma function is^[1]

K(z)=\exp \left(\psi ^{(-2)}(z)+{\frac {z^{2}-z}{2}}-{\frac {z}{2}}\ln(2\pi )\right)

K(z)=Ae^{\psi (-2,z)+{\frac {z^{2}-z}{2}}}

The K-function is closely related to the gamma function and the Barnes G-function; for natural numbers n, we have

K(n)={\frac {(\Gamma (n))^{n-1}}{G(n)}}.

More prosaically, one may write

K(n+1)=1^{1}\,2^{2}\,3^{3}\cdots n^{n}.

The first values are

1, 4, 108, 27648, 86400000, 4031078400000, 3319766398771200000, … ((sequence A002109 in the OEIS)).

References[edit]