本处内容来自：反斗星学量子力学 6.2球谐函数 – 知乎 (zhihu.com)
我觉得了解它算出了什么东西比起它的数学推导、怎么算的要更重要。所以不打算从头算一遍数物里的内容，只把这个过程里的重要部分和结论，简单列一下。
- 数学推导过程
- 球函数性质
- 一点备考笔记
球函数
角动量平方算符 的本征方程可以写为：
算符 的本征值为
，代入
即可得到它的本征值为
其对应的本征波函数为 ，这个函数也就是“球函数”：
- 它的具体形式并不重要，重要的是它的性质。这在《数学物理方法》里面有详细推导过程，此处仅简单罗列结论。
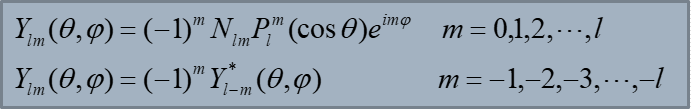
首先，球谐函数的表达式中，出现了 和
两个东西：
是归一化因子，
是连带勒让德多项式。要了解它首先要了解这些内容：
首先，函数 称为勒让德函数，它的一种表达式（微分表示）是：
是微分方程
的解，其中需要作代换
从而使得
。上面这个微分方程是极轴为对称轴（即与变量
无关）的拉普拉斯方程（也就是
）在球坐标下分离变量后得到的。
然后，引申出连带勒让德函数
注意
是连带勒让德函数的符号，
是
最大取到
，因为
是微分方程
的解，它是极轴不为对称轴（即与变量
最后还要注意给上面的多项式做代换
球函数的性质
- 球函数Y是正交归一的：
也就是说，仅当两个球谐函数的
量子数都一致的时候，球谐函数的内积才不为0。算这个交叠积分时，被积变量是
和
- 字母下标
。正如三角函数
可以写作
。
- 球函数
是
和
的共同本征函数，其本征值分别为
和
。
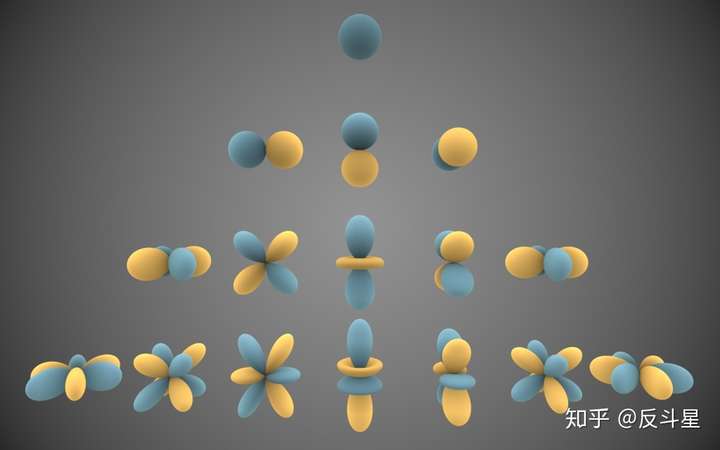
上图从上到下每一行分别对应的就是 的情况，而对于任意一行，从左到右依次对应
。
由于当 的时候，球谐函数是一个常数
，这意味着沿两个角方向的分布一致，也就是此时波函数是一个球形对称的，其等值面是一个球状（如图）。因此图中描绘的是两个量子数不同的取值的情况下的波函数分布等值面。
对应于 的态我们称之为
态，由于一个
不足以完全确定一个态
，不难发现（对每一个确定的
）它是
重简并的。
自身的本征方程
前面的球函数是 和
的共同本征方程，那么其实如果只是求
自己的本征方程的话，是比较简单的。
我们知道
（形式上和
很像对吧）
所以它自己的本征函数就是 对应的本征值是
球谐函数之间的联系（做题备用）
前几个球谐函数的形式可以参考教材，为方便描述，前几个省略表象 ,这里主要讲一下它们的联系：
（考过，默认记得的）
（没归一化）
最后一条也可以写成：（所有等号都没归一化，应该不会考吧，不会吧不会吧）
接下来是中心力场和氢原子的内容了，再到后面就是自旋之类的内容（啊，微扰那里其实还有坑没填上）
