来自维基百科：
http://zh.wikipedia.org/wiki/%E9%BA%A5%E5%8D%A1%E6%89%98%E6%8A%95%E5%BD%B1%E6%B3%95
麦卡托投影法，又称墨卡托投影法、正轴等角圆柱投影，是一种等角的圆柱形地图投影法。本投影法得名于杰拉杜斯·麦卡托，法兰提斯出身的地理学家、地图学家。他于1569年发表长202厘米、宽124厘米以此方式绘制的世界地图。在以此投影法绘制的地图上，经纬线于任何位置皆垂直相交，使世界地图可以绘制在一个长方形上。由于可显示任两点间的正确方位，航海用途的海图、航路图大都以此方式绘制。在该投影中线型比例尺在图中任意一点周围都保持不变，从而可以保持大陆轮廓投影后的角度和形状不变（即等角）；但麦卡托投影会使面积产生变形，极点的比例甚至达到了无穷大。
墨卡托世界地图（1569年）
数学计算
地图上纵向方位（图中的横轴）和纬度（图中的纵轴）的关系。
下列公式定义在使用麦卡托投影的地图中，从纬线φ和经线λ（其中λ0是地图的中央经线）如何推导为坐标系中的点坐标x和y。这是古德曼函数的逆推导：
这是古德曼函数：
比例尺与纬度φ的正割成比例，越趋向极地（φ = ±90°）面积变形越大。此外，由公式可知，极点处的y值为正负无穷大。
麦卡托投影是一种等角投影。
公式推导
假设地球为正球形。（实际上并非为正球形，而是有扁率的，但制作小比例尺地图时误差可忽略不计。若需更精确，可插入等角纬线。）我们需要将经纬度坐标（λ, φ）转换为笛卡尔坐标(x, y)，求以赤道为基准的切柱面投影（即x = λ），并保持形状不变，故：
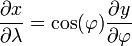
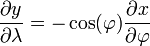
从 x = λ 可知
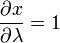
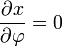
给出
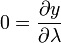
因此，y是φ的唯一函数，且可得到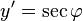
，由积分表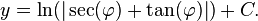
在地图中φ = 0得到y = 0，所以取C = 0.
以麦卡托投影法绘制的地图。
另参见：
参考资料：
- Snyder, John P.. Map Projections – A Working Manual. U.S. Geological Survey Professional Paper 1395. United States Government Printing Office, Washington, D.C. 1987.可至USGS pages下载。
- Monmonier, Mark. Rhumb Lines and Map Wars. Chicago: The University of Chicago Press. 2004.
- Needham, Joseph (1986). Science and Civilization in China: Volume 3; Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books Ltd.
- Needham, Joseph (1986). Science and Civilization in China: Volume 4, Physics and Physical Technology, Part 3, Civil Engineering and Nautics.Taipei: Caves Books Ltd.
