内容来自:http://zh.wikipedia.org/wiki/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E7%82%B9
拉格朗日点(Lagrangian point)又称平动点(libration points)在天体力学中是限制性三体问题的五个特解。就平面圆型三体问题,1767年数学家欧拉根据旋转的二体引力场推算出其中三个点(特解)为L1、L2、L3,1772年数学家拉格朗日推算出另外两个点(特解)为L4、L5。例如,两个天体环绕运行,在空间中有五个位置可以放入第三个物体(质量忽略不计),并使其保持在两个天体的相应位置上。理想状态下,两个同轨道物体以相同的周期旋转,两个天体的万有引力与离心力在拉格朗日点平衡,使得第三个物体与前两个物体相对静止。
五个拉格朗日点之定义如下:
L1
在M1和M2两个大天体的连线上,且在它们之间。
例如一个围绕太阳旋转的物体,它距太阳的距离越近,它的轨道周期就越短。但是这忽略了地球的万有引力对其产生的拉力的影响。如果这个物体在地球与太阳之间,地球引力的影响会减弱太阳对这物体的拉力,因此增加了这个物体的轨道周期。物体距地球越近,这种影响就越大。在L1点,物体的轨道周期恰好等于地球的轨道周期。太阳及日光层探测仪(SOHO)即在日-地系统的L1点上运行。
L2
在两个大天体的连线上,且在较小的天体一侧。
- 例如:相似的影响发生在地球的另一侧。一个物体距太阳的距离越远,它的轨道周期通常就越长。地球引力对其的拉力减小了物体的轨道周期。在L2点,轨道周期变得与地球的相等。
L2通常用于放置空间天文台。因为L2的物体可以保持背向太阳和地球的方位,易于保护和校准。
威尔金森微波各向异性探测器已经在日-地系统的L2点上运行。詹姆斯韦伯太空望远镜将要被放置在日-地系统的L2点上。 嫦娥二号北京时间2011年8月25日23时27分,经过77天的飞行,“嫦娥二号”在世界上首次实现从月球轨道出发,受控准确进入距离地球约150万公里远的、太阳与地球引力平衡点——拉格朗日L2点的环绕轨道。
L3
在两个大天体的连线上,且在较大的天体一侧。
- 例如:第三个拉格朗日点,L3,位于太阳的另一侧,与太阳的距离略小于地球与太阳的距离,但是位于地球轨道的外部,这个看上去矛盾的表述是因为地球公转轨道的中心(严格来说是焦点)是太阳与地球的共同质心,尽管对于日地系统来说共同质心在太阳内部,太阳同时也在围绕这个共同质心转动,所以这种状态成为可能。
一些科幻小说和漫画会在L3点创造一个“反地球” 。
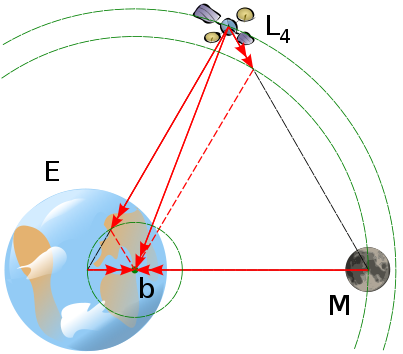
L4
在以两天体连线为底的等边三角形的第三个顶点上,且在较小天体围绕两天体系统质心运行轨道的前方。此点稳定的原因在于,它到两大物体的距离相等,其对两物体分别的引力之比,正好等于两大物体的质量之比。因此,两个引力的合力正好指向该系统的质心,合力大小正好提供该物体公转所需之向心力,使其旋转周期与质量较小天体相同并达成轨道平衡。该系统中,两大物体和L4点上物体围绕质心旋转,旋转中心与质心重合。事实上,L4与L5点上的物体的质量不须小到可忽略。 L4和L5处,小物体受太阳和地球的引力的合力指向日地共同质心且大小正合适。
L4和L5点有时被称为三角拉格朗日点或特洛伊点。
L5
在以两天体连线为底的等边三角形的第三个顶点上,且在较小天体围绕两天体系统质心运行轨道的后方。
L4和L5有时称为三角拉格朗日点或特洛伊点。
- 例如:L4和L5点在地球围太阳运行的轨道之前和之后成60°角处。
实质上是三个物体围绕共同质心转动。
平衡性
严格而言,首先拉格朗日点只算是二星体连线之法平面内的稳定点,而在三维空间内则不稳定:考虑L1:若垂直于中线地推移测试质点,则有一力将其推回平衡点。但若测试质点漂向任一星体,则该星体之引力会将其拉向自己。(类似潮汐力现像。)
L1与L2二点有实际应用:位于此处之卫星只需少量调节便能维持其轨道。
此对比:若M1比M2大于24.96,则L4与L5是真正的穏定点(吸引点):当一测试质点偏离此平衡点,则科里奥利力会将其轨道扭曲成(相对于旋转座标之)扁豆状。太阳-木星系统有几千枚小行星,通称为“特洛伊小行星”,俱划此等轨迹。太阳-火星、太阳-土星、木星-木卫、土星-土卫等系统亦有类似星体。日-地系统中亦有 2010 TK7(第一颗地球特洛伊小行星),在二十世纪五十年代发现了尘雾围绕L4与L5。在地-月系统之L4与L5点亦发现了比对日照更微弱之尘雾。
地球之伴星(companion object)克鲁特尼以类似特洛伊之轨道“围绕”地球,但不是真正的特洛伊卫星。他基本上以一周期略小于一年之椭圆轨道环绕太阳,接近地球时从地球公转提取动能而进入较高之轨道。当克鲁特尼被地球追上,则会交回此动能,跌落低能轨道,重新开始循环。
土卫土卫十一(Epimetheus)与土卫十(Janus)有类似关系,唯因其质量相若,故周期性地互换轨道。
另一类似位形为轨道共振,其中各星体之周期,因其相互作用,成简单整数比,
土卫三(Tethys)的L4和L5点有两个小卫星,土卫十三(Telesto)和土卫十四(Calypso)。土卫四(Dione)的L4点有一个卫星土卫十二(Helene)。
用途
在双星系统、行星和太阳、卫星和行星 (或任何因重力牵引而相互绕行的两个天体) 的轨道面上,所特有的一些稳定点。例如,超前和落后木星轨道60度的地方,各有一个拉格朗日点,如果有小行星在这两个拉格朗日点上,它会在此点附近振荡,但不会离开这些点,而特洛伊小行星 (Trojan asteroids) 就是位在这两个区域。事实上,任何「双星系统」都有五个拉格朗日点。除了上面的两个点之外,另三个的拉格朗日点不很稳定,位在其他拉格朗日点上的小天体,稍受扰动就会离开它位置。
在天体力学中,拉格朗日点是限制性三体问题的5个特解。例如,两个天体环绕运行,在空间中有5个位置可以放入第三个物体(质量忽略不计),并使其保持在两个天体的相应位置上。理想状态下,两个同轨道物体以相同的周期旋转,两个天体的万有引力提供在拉格朗日点需要的向心力,使得第三个物体与前两个物体相对静止。
理性在太空闪光
按照计划,美国国家航空航天局要对哈勃空间望远镜(HST)进行第5次维修。维修之后,人们估计它至少能够再工作5年。HST一时还不“退休”,“继任者”詹姆斯·韦伯空间望远镜(JWST)只好在地面上再静候几年了。
有趣的是,詹姆斯·韦伯空间望远镜将不像HST那样绕着地球公转,它的“工作地点”被定在太阳-地球系统的“第二拉格朗日点”(在地球背向太阳一面的150万千米处)。拉格朗日(1736—1813)怎么也想不到,他的“三体问题”研究成果,在发表200多年之后,屡次在人类的科学研究与航天工程中被引用。
“三体问题”研究成果被后人使用,JWST不是第一例。更早受到世界瞩目的是2001年升空的威尔金森宇宙微波各向异性探测卫星(WMAP),WMAP是继宇宙微波背景探索者卫星COBE之后的第二代宇宙微波背景探测卫星。人们感到好奇的,也是WMAP的定位:处于太阳-地球系统的“第二拉格朗日点”。
现在,让我们说一说,什么是“三体问题”?简单地说,就是“太阳-地球-小质量物体”,或者“太阳-木星—小质量物体”这样的“三个天体”的系统如何运行。说得详细一点,就是研究这样的问题:“太阳-地球”或者“太阳-木星”这些天体系统,如果有无限小质量的物体加入进来,那么在万有引力作用下,这些小物体会怎样运动?
“三体问题中”最简单的一种类型,是“平面圆形限制三体问题”。拉格朗日求解这个问题,得到了5个特解:3个直线解和两个等边三角形解,只有两个等边三角形解是稳定解。如果小质量物体处在某一个拉格朗日点上,那么它所受到的太阳-木星(或太阳-地球)的引力,恰好等于它与太阳-木星(或太阳-地球)一起转动时所需要的向心力。这就是说,处在某一个拉格朗日点上,小质量物体就可与太阳-木星(或太阳-地球)的相对位置保持不变。
有趣的是,“第一代卫星”HST和COBE都是绕着地球“公转”,“第二代卫星”JWST和WMAP都把位置定在太阳-地球系统的“第二拉格朗日点”。欧洲空间局的两颗卫星“赫歇尔”、“GAIA”也看好那个“地点”,计划到那里落户。
在科学发展的历史上,跟“三体问题”有关的好玩故事还有不少。大约一百年前,1906年,德国天文学家马克思·沃尔夫发现了一颗奇异的小行星。它的轨道与木星相同,而不在通常所说火星轨道与木星轨道之间的小行星带里。最奇妙的是,它的绕日运动周期与木星相同。从太阳看去,它总是在木星之前60°运转,不会与木星贴近。这颗小行星被命名为“阿基里斯”,他是荷马史诗《伊里亚特》叙述的特洛伊战争中的希腊英雄。
天文学家沙利叶敏感地意识到,小行星“阿基里斯”很可能是法国数学家拉格朗日“三体问题”的一个特例:只要小物体、大行星与太阳这三者形成一个等边三角形,这小物体和大行星就会永远同步地绕太阳旋转,它们永远不会相撞。
果然,天文学家很快就在木星之后60°的位置上,也发现了小行星。迄今为止,在木星前后这两个拉格朗日点上,已找到700颗小行星。科学理论的预见何其美妙!后来发现的这些处在拉格朗日点上的小行星,都以特洛伊战争里的英雄命名。于是,这几百颗小行星,就有了一个“集体的”称号:特罗央群小行星。这个“特罗央”,实际上就是古希腊神话中小亚细亚的“特洛伊”城。
不久前,法国空间研究中心的天文学家提出一个新设想,使得拉格朗日点将来可能获得新的用途:用作拦截危险小行星的布防点。法国科学家提出,捕获一些中等体积的“天体”,把它们“部署”到“太阳—地球”体系的五个拉格朗日点中的一个。发现对地球有危险的小行星以后,人们可以调用这些“天体”去拦截危险小行星。
美妙的理论、美丽的图像、美好的应用,拉格朗日带给我们的兴趣是全方位的:理趣、情趣、志趣。这是我们对科学的全面的美感。