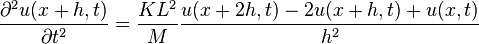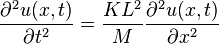一维波动方程可用如下的方式推导:一列质量为m的小质点,相邻质点间用长度h的弹簧连接。弹簧的弹性系数(又称“倔强系数”)为k:
其中u(x) 表示位于x的质点偏离平衡位置的距离。施加在位于x+h 处的质点m 上的力为:
其中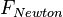 代表根据牛顿第二定律计算的质点惯性力,
代表根据牛顿第二定律计算的质点惯性力,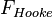 代表根据胡克定律计算的弹簧作用力。所以根据分析力学中的达朗贝尔原理,位于x+h 处质点的运动方程为:
代表根据胡克定律计算的弹簧作用力。所以根据分析力学中的达朗贝尔原理,位于x+h 处质点的运动方程为:
式中已注明u(x) 是时间t 的显函数。
若N 个质点间隔均匀地固定在长度L = N h 的弹簧链上,总质量M = N m,链的总体劲度系数为K = k/N,我们可以将上面的方程写为:
取极限 N 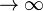 , h
, h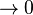 就得到这个系统的波动方程:
就得到这个系统的波动方程:
在这个例子中,波速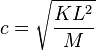 。
。
内容来自维基百科,查看更多请访问:http://zh.wikipedia.org/wiki/%E6%B3%A2%E5%8A%A8%E6%96%B9%E7%A8%8B


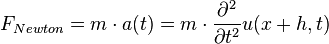
![F_{Hooke} = F_{x+2h} + F_x = k \left [ {u(x+2h,t) - u(x+h,t)} \right ] + k[u(x,t) - u(x+h,t)]](http://upload.wikimedia.org/math/2/7/a/27a416175f8c2da3c21ca1d325bebb54.png)
![m{\partial^2u(x+h,t) \over \partial t^2}= k[u(x+2h,t)-u(x+h,t)-u(x+h,t)+u(x,t)]](http://upload.wikimedia.org/math/4/b/6/4b6e13f0f6afda0c53a6dae55607cb40.png)