克莱因-戈尔登方程
薛定谔方程并没有将相对论效应纳入考虑范围内。对于伽利略变换，薛定谔方程是不变的。 对于洛伦兹变换，薛定谔方程的形式会改变。为了要涵盖相对论效应，必须修改薛定谔方程。试想能量-动量关系式（energy-momentum relation），
；
是
是将这关系式内的能量与动量改为其对应的算符，将整个关系式作用于波函数，可以得到
。
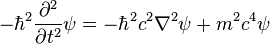稍加编排，可以得到克莱因-戈尔登方程：
；
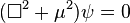其中，
是达朗贝尔算符，
。
对于洛伦兹变换，这方程的形式不会改变，是洛伦兹不变式。但是，它是一个时间的二阶微分方程，不能成为波函数的方程。另外，这方程的解拥有正频率和负频率。平面波波函数解的色散关系式为
；
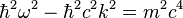其中，
是角频率，可以是正值或负值。
对量子力学来说，正负角频率或正负能量，是一个很严峻的问题，因为无法从底端限制能量的最低值。虽然如此，加以适当的诠释，这方程仍旧能够正确地给出零自旋粒子的相对论性波函数。
狄拉克方程
狄拉克方程乃是时间的一阶微分方程，专门描述自旋-½粒子的波函数：
，
、
分别是空间、时间。狄拉克方程仍旧存在负能量的解。为了要除去这麻烦的瑕疵，必须把波动方程当作一个量子场的方程，而不是一个波函数的方程。因为，相对论与单粒子图案互不相容。一个相对论性粒子不能被局限于一个小区域，除非粒子的数量变为无穷多。
假设一个粒子被局限于一个长度为 
的一维盒子里，根据不确定性原理，动量的不确定性 
。假若，因为粒子的动量足够的大，质量可以被忽略，则能量的不确定性大约为 
。当盒子的长度 等于康普顿波长 
时，能量的不确定性等于粒子的质能（mass energy）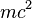 
。当盒子的长度 小于康普顿波长时，无法确定盒子内只有一个粒子，因为用来测量盒子内粒子位置的机制，也可以从制造出更多的粒子。
查看更多：http://zh.wikipedia.org/wiki/%E8%96%9B%E5%AE%9A%E8%B0%94%E6%96%B9%E7%A8%8B
